This research was independently conducted by me and my collaborator Jialu Xu during the first semester of our junior year in the “College Physics Experiment” course. We conducted a survey of the experimental background, designed the experimental procedure, and utilized teaching instruments for our experiments.
Abstract
The application of gamma ray ranging in spacecraft landings is investigated in this study. Secondary gamma rays, characterized by high frequency and energy, are evaluated for their penetration capabilities, a crucial factor in spacecraft landing accuracy and safety. The experimental setup comprises a gamma source, detector, and copper sheets. Key challenges include photon obstruction and finite copper size, addressed through the Monte Carlo method for data correction. Results indicate the potential of gamma ray altimeters in spacecraft landings, demonstrating a significant improvement in landing reliability. The study contributes to the field of space exploration by proposing an alternative method to traditional landing sensors, enhancing the safety and accuracy of spacecraft descent.
Introduction
Gamma Rays
Gamma rays are a form of electromagnetic radiation, like light and X-rays, but with much shorter wavelengths and higher energies. They are produced by various processes in the universe, including the decay of radioactive substances and certain types of nuclear reactions. Gamma rays can penetrate most materials, making them useful in medical imaging and treatment, as well as in industrial applications.
Penetration of Matter
Gamma rays possess a unique ability to penetrate matter due to their high energy and short wavelength.
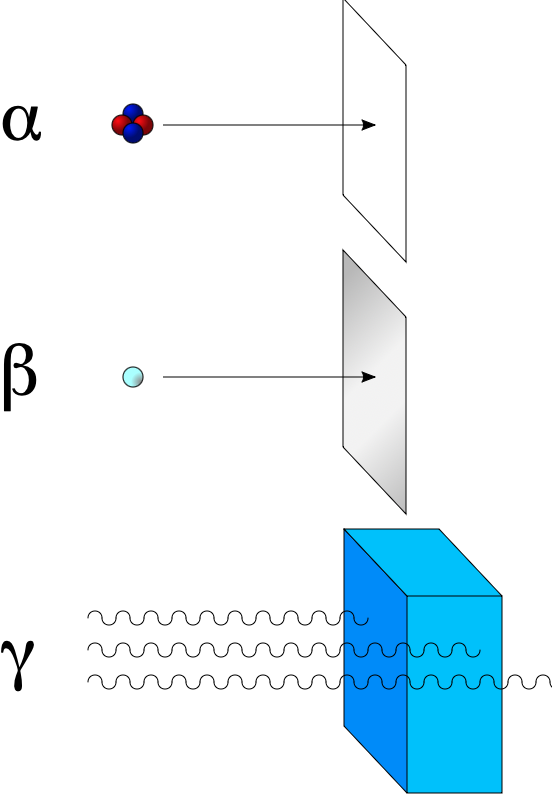
Figure 1.. Alpha radiation consists of helium nuclei and is readily stopped by a sheet of paper. Beta radiation , consisting of electrons or positrons , is stopped by an aluminum plate, but gamma radiation requires shielding by dense material such as lead or concrete.
Matter Interaction
The interaction between γ photons and matter mainly includes the Compton effect , photoelectric effect , and pair production .
For γ photons of different energies and stopping media, the roles played by the photoelectric effect, Compton scattering, and pair production differ. Figure 2. illustrates the relations between these three effects and the atomic number (Z) of the absorbing material as well as the photon energy.
Figure 3.. The relations between the three effects and the atomic number of the absorber, as well as the photon energy. According to Figure 4., it can be observed that for low-energy γ rays and absorbers with high atomic numbers, the photoelectric effect is dominant. For medium-energy γ rays and absorbers with low atomic numbers, Compton scattering is predominant. For high-energy γ rays and absorbers with high atomic numbers, the pair production effect is dominant.
In our investigation, photons with an energy of 0.662 MeV are released by the γ source ( \(^{137}\text{Cs}\)). When these photons interact with electrons in copper (Cu), characterized by lower atomic numbers, the predominant process is Compton scattering, accompanied by a minor contribution from the photoelectric effect.
Spacecraft Landings and Advantages of Gamma Ray Ranging
Manned spaceflight and deep-space exploration involve critical Entry, Descent, and Landing (EDL) processes, crucial for returning to Earth or landing on celestial bodies. These processes necessitate precise control of landing speed, especially for manned spacecraft where personal safety and spacecraft reliability are paramount.
One key element in EDL is the retrograde landing rocket, which employs functionally graded materials to enhance its properties. Traditional landing sensors, such as Doppler radar, radar altimeters, and laser altimeters, are used to measure altitude during landing. However, these sensors can be significantly affected by atmospheric conditions
Notably, the γ photons altimeter, exemplified by the Russian “KAKTUS,” presents a valuable alternative. This technology emits gamma photons over an area and accurately measures the altitude by receiving the scattered photons, allowing for controllable landings, even at low altitudes.
In contrast to laser or mechanical touch altimeters that measure altitude for specific points, the γ photons altimeter (Figure [alm label=’altimeter’]) can measure average altitudes, reflecting the real landing point within a certain region. An additional advantage lies in the strong penetrability of γ rays, minimizing interference from dust raised by the engine during the landing process.
In a previous study
\[
In theory, the calculation of \(\phi_p\) allows us to derive an h-f curve, where ‘h’ represents altitude or distance to the ground, and ‘f’ signifies the frequency, indicating the number of gamma photons detected within a second. Nevertheless, applying the aforementioned formula directly proves challenging in the context of a practical altimeter system, owing to its complexity. Therefore, the h-f curve is alternatively established through experimental means, as depicted in Figure [alm label=’h-f’].
Figure 5.. The physical process of altitude measurement.
Figure [alm label=’h-f’]. The static h-f curve measured in previous experiments by Liu et al.
Objectives
The objective of our study is to explore the feasibility and accuracy of using gamma rays for spacecraft landing applications. Specifically, the study aims to:
Investigate the Penetrative Properties of Secondary Gamma Rays : Understand how secondary gamma rays interact with different materials and their ability to penetrate surfaces, which is crucial for accurate ranging.Evaluate the Efficiency of Gamma Ray Ranging : Assess how effectively gamma ray ranging can measure distances, especially in the challenging environments encountered during spacecraft landings.Overcome Experimental Challenges : Address and find solutions for specific challenges such as photon obstruction and the finite size of the copper reflector used in the experiment.Apply Corrective Techniques for Enhanced Precision : Utilize the Monte Carlo method to correct experimental data, aiming to improve the accuracy and reliability of gamma ray ranging measurements.Demonstrate the Potential for Spacecraft Landing Applications : Show through experimental results and analysis that gamma ray ranging can significantly enhance the precision and safety of spacecraft landings, contributing to the advancement of space exploration technology.
Experimental Approach
Experimental Arrangement
The apparatus is listed as follows (see Figure 6.).
Gamma Source (\(^{137}\text{Cs}\)): Emits \(\gamma\) photons with an energy of 0.622 MeV.
Detector (Scintillation Probe): Detects and converts \(\gamma\) photons into electrical signals for analysis.
Lead Brick: Positioned between the source and the detector, serving as a barrier that prevents direct penetration of γ rays to the detector.
Copper Sheets: Stopping media for \(\gamma\) rays, primarily undergoing Compton scattering.
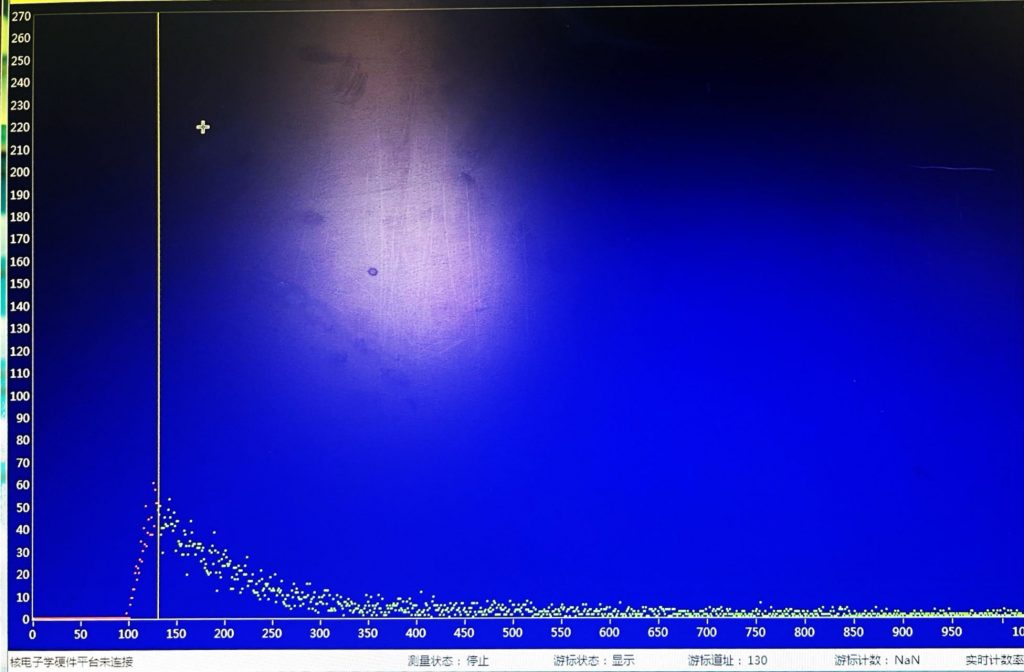
Multichannel Data Processing Software: Efficiently manages data from multiple channels, enabling analysis and interpretation. Provides the intensity of photons with varying energy, generating \(\gamma\) spectra (see Figure 7.).
Computer: Central processing unit for data acquisition, storage, and analysis, coordinating information from various components in the experiment.
Figure 8.. Image of experimental arrangement. Figure 9.. Software-provided spectrum: X-axis corresponds to channel number (proportional to photon energy E), Y-axis to intensity (proportional to photon count).
Ensure precise placement of the source, detector, and lead brick as depicted in the image.
Placing the lead brick too close to the detector obstructs most scattered rays.
Placing the lead brick too far back allows unwanted \(\gamma\) rays to leak directly towards the detector, intensifying fluctuations more than scatterings and causing significant errors.
Principle
The principle of the experiment is based on the observation that as the distance between the source and copper plates increases, the quantity of photons experiencing Compton backscattering from the copper plates and subsequently detected decreases. This reduction leads to a diminished number of received photons, resulting in a weaker signal. This observed correlation has been utilized to construct a curve that can be effectively employed for real-world distance measurements.
It’s worth noting that Compton backscattering can colloquially be referred to as ‘reflection’ due to the geometric similarities between backscattering and reflection. However, it’s essential to emphasize that Compton backscattering is fundamentally distinct from light reflection in terms of underlying physical principles, representing distinct interactions of matter.
Figure 10.. Experimental Apparatus Setup
Figure 11.. Photons counting corresponding to different distances.
Procedure
To obtain an ‘I-h’ curve, we follow this experimental procedure for each copper distance \(h\):
Setting Up the Experiment – Mirror and Copper Orientation: Place the plain mirror directly in front of the copper plates and adjust the orientation of both the plain mirror and the copper plates using a laser pen positioned atop the gamma source. Ensure that emitted photons from the source effectively reach the detector.Data Collection with the Software – Recording Gamma Ray Intensity: Utilize the Multichannel Data Processing Software to record the intensity of gamma rays received by the detector over a period of \(T\) seconds, denoted as \(I_1(E)\). It’s important to note that the software provides a spectrum, indicating that \(I_1\) is a function of \(E\).Background Signal Measurement – Obtaining Detector’s Background Signal: Remove the copper and repeat step (2) to obtain the background signal of the detector, referred to as \(I_0(E)\).Calculating Scattered Gamma Rays – Determining Intensity of Scattered Gamma Rays: Represent the intensity of reflected gamma rays as \(I_r(E) = I_1(E) – I_0(E)\).Total Intensity Calculation – Computing the Total Gamma Ray Intensity: Express the total intensity \(I\) as an integral over \(E\), i.e., \(I = \int_{E_1}^{E_2} I_r(E) \, \text{d}E\), where \([E_1, E_2]\) defines the energy range of reflected gamma photons that undergo Compton scattering. For our purposes, assume \([E_1, E_2] = [0.13 MeV, 0.25 MeV]\).
Challenges and Solutions
Data Correction for Lead Block Obstruction
As the distance decreased, lead blocks obstructed photons, reducing the number received by the probe. This required corrections for close-range scenarios.
Figure 12.. Photons reflected at specific angles are obstructed by the lead block.
Figure 13.. The intensity of gamma rays with respect to the emission angle θ follows a normalized distribution function f(θ).
However, challenges arise when attempting to accurately calculate the number of gamma photons obstructed by the block. The complexity of the experimental setup is a major factor, as it requires moving copper plates between different distances to obtain an ‘I-h’ curve. Furthermore, the emitted gamma rays are not collimated. The intensity of gamma rays, concerning the emission angle θ, conforms to a normalized distribution function denoted as f(θ). Likewise, the intensity of gamma rays reflected by the copper foil also adheres to a normalized distribution function represented by g(θ).
To gain a more intuitive understanding of the challenge associated with analytically calculating the number of obstructed photons, we embark on a derivation here. Let us set the stage by defining the pertinent variables:
First, we have the photon angle distribution originating from the source, denoted as \( f(\theta) \), and the photon angle distribution after reflection by a copper plate, expressed as \( g(\theta’) \).
If we consider photons that are reflected at angles falling within the range from \( \theta’_1 \) to \( \theta’_2 \) and subsequently reach a detector, we can formulate the number of received photons, \( dN_{\text{received}}(\theta) \), as follows:
\[dN_{\text{received}}(\theta) = \text{d}N'(\theta) \int_{\theta_1′(\theta)}^{\theta_2′(\theta)} g(\theta’)\text{d}\theta’\]
Further integrating this expression, we obtain:
\[N_{\text{received}} = \int \int_{\theta_1′(\theta)}^{\theta_2′(\theta)} g(\theta’)\text{d}\theta’ \text{d}N'(\theta) = N_0 \int \int_{\theta_1′(\theta)}^{\theta_2′(\theta)} g(\theta’)\text{d}\theta’ f'(\theta) \text{d}\theta\]
Here, \( \theta \) signifies the angle of photon emission from the source, and it is important to note that both \( \theta’_1 \) and \( \theta’_2 \) should be considered as functions of \( \theta \) and the distance of the copper plates.
In situations where no obstructions are present, it becomes necessary to rederive the expressions for \( \theta’_1 \) and \( \theta’_2 \), thus highlighting the intricacies involved in this analytical pursuit.
Data Correction for Finite Copper Size
In an actual spacecraft landing scenario, the land that reflects gamma rays can be approximated as infinitely vast. Nevertheless, our experimental copper sample is confined to finite dimensions, resulting in a diminished reflection of gamma photons. Therefore, the necessity arises for a correction to account for the infinite land conditions.
Monte Carlo Method
The Monte Carlo Method, a versatile, precise, and time-efficient statistical technique, finds application in simulating photon emission and assessing photon obstructions by lead blocks. This method offers the flexibility to fine-tune particle number integration outcomes. Here is a breakdown of the method’s procedure:
Modeling the Angular Distribution: The method employs a normal distribution to mathematically represent the angular distribution of emitted and reflected photons. In the case of emission, this distribution is expressed as \( f(\theta) = Ae^{-\frac{\theta^2}{2\sigma^2}} \), where \(\theta\) denotes the angle of emission, with \(\sigma\) set to \(\pi/6\) to ensure that the probability of \( \theta \) falling within the range of \((- \frac{\pi}{2}, \frac{\pi}{2})\) reaches a substantial 99.7%; in the case of reflection, it is represented as \( g(\theta’) = Ae^{-\frac{(\theta’-\theta_0)^2}{2\sigma^2}} \) with \(\theta_0\) being the incident angle and \(\theta’\) the reflection angle.Computer Simulation: A computer simulation is conducted to emulate the emission of photons based on the aforementioned angular distribution. This simulation rigorously evaluates the potential obstructions encountered by photons as they interact with lead blocks, taking into account the measured geometric relations.Photon Quantity Assessment: The method tracks and records the quantity of photons that successfully reach the scintillation probe under two distinct conditions: one in the presence of the lead block with a finite-sized copper sample and the other in the absence of the lead block with an infinitely sized copper sample. These quantities are denoted as \( N_1 \) and \( N_2 \), respectively.Integration Correction: To ensure the accuracy of the integral results derived directly from the Multichannel Data Processing Software, a correction is applied. This correction is implemented using the formula \( N = \frac{N_2}{N_1} \times N_{\text{baseline}} \).
Results and Discussion
The I-h Curve
After performing the aforementioned experimental procedure and integrating \(I_r(E)\) over E, we derive an initial I-h curve, as illustrated in Figure [alm label=’primordial’]. Furthermore, employing the Monte Carlo rectification method, we calculate a correction factor denoted as \(N_2/N_1\), as depicted in Figure [alm label=’correction factor’].
Figure [alm label=’primordial’]. Primordial I-h curve obtained directly from the experimental procedure.
Figure [alm label=’correction factor’]. The curve of correction factor (ratio) varying with distance h.
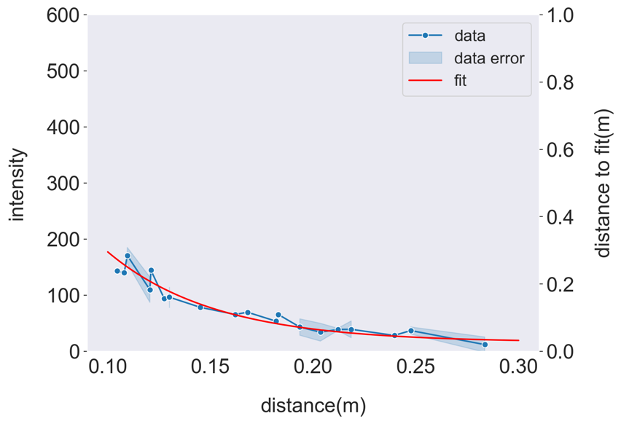
Consequently, by multiplying the initial I-h curve by the correction factor, we obtain the rectified curve, which can be fitted and expressed as \(y=43694e^{-44.2x}+48\), as shown in Figure [alm label=’final’]. The fitted curve exhibits a relatively small error, with a maximum approximation of 40. This curve corresponds closely in terms of the exponential relationship to the curve obtained from the gamma photon altimeter measurements, depicted in Figure [alm label=’h-f’], which can be fitted and expressed as \(y=132e^{-0.730x}+15\). Furthermore, the plot reveals that the gamma ray altimeter we have constructed exhibits remarkable precision within the range of [0.10 m, 0.15 m], where the ‘I’ curve experiences a rapid decrease, indicating the sensitivity of ‘I’ to ‘h’ within this specific range.
Figure [alm label=’final’]. The rectified I-h curve. Ranging Earth Sample
We have obtained an earth sample with the specific purpose of utilizing it to mimic the terrestrial ground surface encountered during a spacecraft landing. This Earth sample is composed of distinct layers, encompassing loose leaves on the upper surface, soil beneath, and a sturdy stone slab at the base (refer to Figure [alm label=’earth sample’]). The leaves, owing to their loose arrangement, effectively simulate the non-load-bearing layers that cannot withstand the spacecraft’s weight. In contrast, the soil and the stone slab exhibit greater rigidity, faithfully replicating the weight-bearing layers found on a genuine landing surface. It is noteworthy that these materials consist primarily of light atoms, such as hydrogen (H), carbon (C), oxygen (O), aluminum (Al), magnesium (Mg), and calcium (Ca). Consequently, when it comes to gamma ray interactions, Compton scattering prevails as the dominant mechanism among the three types of matter interactions.
After correctly positioning the earth sample and following the previously mentioned procedure, we obtained \(I’\) as the intensity of gamma rays “reflected” (i.e., inversely scattered) by the sample. Using the ‘I-h’ curve we had previously obtained, we determined the distance of the sample to the detector (‘h’). The relationships between the gamma ray-measured distance (‘distance by gamma’), the distance to the stone slab (‘distance to stone’), and the distance to the surface of leaves (referred to as ‘distance by laser’ because the laser reflects off the surface of the leaves) are illustrated in Figure [alm label=’relation dist’].
Figure [alm label=’earth sample’]. Earth sample to be ranged.
Figure [alm label=’relation dist’]. The relation between ‘distance by gamma’, ‘distance to stone’ and ‘distance by laser’.
As depicted in the figure, the inverse scattering of gamma photons in the earth sample can be equivalently represented as a reflection from the soil layer. Since the soil layer is considered weight-supportive, the gamma ray-ranging results accurately reflect the actual landing point.
Conclusion
The research presented herein confirms the viability of gamma ray ranging as a transformative approach for spacecraft landings. Despite encountering obstacles such as photon obstruction and the limited size of the copper reflector, the application of advanced corrective techniques like the Monte Carlo method has validated the effectiveness and reliability of this novel method. The corrected I-h curves underscore the enhanced precision achievable with gamma ray altimeters, paving the way for safer and more accurate space missions. This breakthrough in landing technology promises to contribute to the evolution of space exploration.
References
{13285244:23UZQZXH};{13285244:TA3NBB35};{13285244:PLPBIUMM};{13285244:CW3TGCI5};{13285244:TA3NBB35};{13285244:DPIN5N5W};{13285244:V4U8ZCMN},{13285244:7FK2REVH},{13285244:8EMK69KH};{13285244:N33B7459},{13285244:VVAWSPFB},{13285244:CKNXM3ZM},{13285244:CUFKV4PS};{13285244:YUMCLWRE};{13285244:YUMCLWRE};{13285244:DPIN5N5W}
nature
default
asc
0
197
%7B%22status%22%3A%22success%22%2C%22updateneeded%22%3Afalse%2C%22instance%22%3Afalse%2C%22meta%22%3A%7B%22request_last%22%3A50%2C%22request_next%22%3A50%2C%22used_cache%22%3Atrue%7D%2C%22data%22%3A%5B%7B%22key%22%3A%22NJ9JJYY9%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ye%20et%20al.%22%2C%22parsedDate%22%3A%222021%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EYe%2C%20W.%2C%20Wu%2C%20H.%2C%20Tan%2C%20Z.%20%26amp%3B%20Zou%2C%20Q.%20An%20Adaptive%20Time%20Stepping%20Algorithm%20and%20Its%20Application%20to%20Platelet%20Aggregation%20Simulation.%20in%20%3Ci%3E2021%20IEEE%20Intl%20Conf%20on%20Parallel%20%26amp%3B%20Distributed%20Processing%20with%20Applications%2C%20Big%20Data%20%26amp%3B%20Cloud%20Computing%2C%20Sustainable%20Computing%20%26amp%3B%20Communications%2C%20Social%20Computing%20%26amp%3B%20Networking%20%28ISPA%5C%2FBDCloud%5C%2FSocialCom%5C%2FSustainCom%29%3C%5C%2Fi%3E%201360%26%23×2013%3B1369%20%28IEEE%2C%20New%20York%20City%2C%20NY%2C%20USA%2C%202021%29.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27http%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1109%5C%2FISPA-BDCloud-SocialCom-SustainCom52081.2021.00186%27%3Ehttp%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1109%5C%2FISPA-BDCloud-SocialCom-SustainCom52081.2021.00186%3C%5C%2Fa%3E.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22conferencePaper%22%2C%22title%22%3A%22An%20Adaptive%20Time%20Stepping%20Algorithm%20and%20Its%20Application%20to%20Platelet%20Aggregation%20Simulation%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Weicai%22%2C%22lastName%22%3A%22Ye%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Hao%22%2C%22lastName%22%3A%22Wu%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Zhijun%22%2C%22lastName%22%3A%22Tan%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Qingsong%22%2C%22lastName%22%3A%22Zou%22%7D%5D%2C%22abstractNote%22%3A%22In%20this%20paper%2C%20we%20propose%20an%20adaptive%20strategy%20on%20the%20choice%20of%20time%20step%20size%20for%20the%20Velocity%20Verlet%20%28VV%29%20algorithm.%20The%20key%20idea%20here%20is%20to%20adjust%20the%20time%20step%20size%20adaptively%20according%20to%20the%20velocity%20and%20position%20of%20each%20pair%20of%20particles.%20The%20Adaptive%20Time%20Stepping%20Velocity%20Verlet%20%28ATS-VV%29%20algorithm%20is%20then%20applied%20to%20the%20Coarse%20Grained%20Molecular%20Dynamics%20%28CGMD%29%20simulation%20for%20the%20platelet%20aggregation%20process.%20Several%20numerical%20experiments%20show%20that%20the%20adaptive%20strategy%20not%20only%20enhances%20the%20e%5Cufb03ciency%20of%20the%20standard%20VV%20algorithm%2C%20but%20also%20improves%20the%20fault-tolerant%20ability%20of%20the%20simulation%20program.%20In%20particular%2C%20our%20adaptive-time-step%20size%20simulation%20takes%20only%20time%20steps%20ranged%20from%200.7%25%20to%2019%25%20of%20the%20standard%20VV%20algorithm%20with%20the%20same%20%5Cufb01nest%20time%20step%20size.%22%2C%22date%22%3A%229%5C%2F2021%22%2C%22proceedingsTitle%22%3A%222021%20IEEE%20Intl%20Conf%20on%20Parallel%20%26%20Distributed%20Processing%20with%20Applications%2C%20Big%20Data%20%26%20Cloud%20Computing%2C%20Sustainable%20Computing%20%26%20Communications%2C%20Social%20Computing%20%26%20Networking%20%28ISPA%5C%2FBDCloud%5C%2FSocialCom%5C%2FSustainCom%29%22%2C%22conferenceName%22%3A%222021%20IEEE%20Intl%20Conf%20on%20Parallel%20%26%20Distributed%20Processing%20with%20Applications%2C%20Big%20Data%20%26%20Cloud%20Computing%2C%20Sustainable%20Computing%20%26%20Communications%2C%20Social%20Computing%20%26%20Networking%20%28ISPA%5C%2FBDCloud%5C%2FSocialCom%5C%2FSustainCom%29%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1109%5C%2FISPA-BDCloud-SocialCom-SustainCom52081.2021.00186%22%2C%22ISBN%22%3A%22978-1-66543-574-1%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fieeexplore.ieee.org%5C%2Fdocument%5C%2F9644767%5C%2F%22%2C%22collections%22%3A%5B%22A7A2VE5G%22%5D%2C%22dateModified%22%3A%222024-02-22T08%3A37%3A40Z%22%7D%7D%2C%7B%22key%22%3A%22SL9NYGQT%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Shi%20et%20al.%22%2C%22parsedDate%22%3A%222019%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EShi%2C%20Y.%20%3Ci%3Eet%20al.%3C%5C%2Fi%3E%20Study%20of%20adaptive%20symplectic%20methods%20for%20simulating%20charged%20particle%20dynamics.%20%3Ci%3EJournal%20of%20Computational%20Dynamics%3C%5C%2Fi%3E%20%3Cb%3E6%3C%5C%2Fb%3E%2C%20429%26%23×2013%3B448%20%282019%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Study%20of%20adaptive%20symplectic%20methods%20for%20simulating%20charged%20particle%20dynamics%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Yanyan%22%2C%22lastName%22%3A%22Shi%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Yajuan%22%2C%22lastName%22%3A%22Sun%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Yulei%22%2C%22lastName%22%3A%22Wang%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jian%22%2C%22lastName%22%3A%22Liu%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22name%22%3A%22%2CLSEC%2C%20ICMSEC%2C%20Academy%20of%20Mathematics%20and%20Systems%20Science%2C%20CAS%2C%20Beijing%20100190%2C%20China%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22name%22%3A%22%2CSchool%20of%20Mathematical%20Sciences%2C%20University%20of%20Chinese%20Academy%20of%20Sciences%2C%20Beijing%20100049%2C%20China%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22name%22%3A%22%2CDepartment%20of%20Engineering%20and%20Applied%20Physics%2C%20USTC%2C%20Hefei%2C%20Anhui%20230026%2C%20China%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22name%22%3A%22%2CKey%20Laboratory%20of%20Geospace%20Environment%2C%20CAS%2C%20Hefei%2C%20Anhui%20230026%2C%20China%22%7D%5D%2C%22abstractNote%22%3A%22In%20plasma%20simulations%2C%20numerical%20methods%20with%20high%20computational%20e%5Cufb03ciency%20and%20long-term%20stability%20are%20needed.%20In%20this%20paper%2C%20symplectic%20methods%20with%20adaptive%20time%20steps%20are%20constructed%20for%20simulating%20the%20dynamics%20of%20charged%20particles%20under%20the%20electromagnetic%20%5Cufb01eld.%20With%20speci%5Cufb01cally%20designed%20step%20size%20functions%2C%20the%20motion%20of%20charged%20particles%20con%5Cufb01ned%20in%20a%20Penning%20trap%20under%20three%20di%5Cufb00erent%20magnetic%20%5Cufb01elds%20is%20studied%2C%20and%20also%20the%20dynamics%20of%20runaway%20electrons%20in%20tokamaks%20is%20investigated.%20The%20numerical%20experiments%20are%20performed%20to%20show%20the%20e%5Cufb03ciency%20of%20the%20new%20derived%20adaptive%20symplectic%20methods.%22%2C%22date%22%3A%222019%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.3934%5C%2Fjcd.2019022%22%2C%22ISSN%22%3A%222158-2505%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Faimsciences.org%5C%2F%5C%2Farticle%5C%2Fdoi%5C%2F10.3934%5C%2Fjcd.2019022%22%2C%22collections%22%3A%5B%22A7A2VE5G%22%5D%2C%22dateModified%22%3A%222024-02-20T03%3A49%3A59Z%22%7D%7D%2C%7B%22key%22%3A%22JKP3ENIP%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Qiao%20et%20al.%22%2C%22parsedDate%22%3A%222011%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EQiao%2C%20Z.%2C%20Zhang%2C%20Z.%20%26amp%3B%20Tang%2C%20T.%20An%20Adaptive%20Time-Stepping%20Strategy%20for%20the%20Molecular%20Beam%20Epitaxy%20Models.%20%3Ci%3ESIAM%20J.%20Sci.%20Comput.%3C%5C%2Fi%3E%20%3Cb%3E33%3C%5C%2Fb%3E%2C%201395%26%23×2013%3B1414%20%282011%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22An%20Adaptive%20Time-Stepping%20Strategy%20for%20the%20Molecular%20Beam%20Epitaxy%20Models%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Zhonghua%22%2C%22lastName%22%3A%22Qiao%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Zhengru%22%2C%22lastName%22%3A%22Zhang%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tao%22%2C%22lastName%22%3A%22Tang%22%7D%5D%2C%22abstractNote%22%3A%22This%20paper%20is%20concerned%20with%20the%20numerical%20simulations%20for%20the%20dynamics%20of%20the%20molecular%20beam%20epitaxy%20%28MBE%29%20model.%20The%20numerical%20simulations%20of%20the%20MBE%20models%20require%20long%20time%20computations%2C%20and%20therefore%20large%20time-stepping%20methods%20become%20necessary.%20In%20this%20work%2C%20we%20consider%20some%20unconditionally%20energy%20stable%20%5Cufb01nite%20di%5Cufb00erence%20schemes%2C%20which%20will%20be%20used%20in%20the%20time%20adaptivity%20strategies.%20It%20is%20found%20that%20the%20use%20of%20the%20time%20adaptivity%20cannot%20only%20resolve%20the%20steady-state%20solutions%20but%20also%20the%20dynamical%20changes%20of%20the%20solution%20accurately%20and%20e%5Cufb03ciently.%20The%20adaptive%20time%20step%20is%20selected%20based%20on%20the%20energy%20variation%20or%20the%20change%20of%20the%20roughness%20of%20the%20solution.%20The%20numerical%20experiments%20demonstrated%20that%20the%20CPU%20time%20is%20signi%5Cufb01cantly%20saved%20for%20long%20time%20simulations.%22%2C%22date%22%3A%2201%5C%2F2011%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1137%5C%2F100812781%22%2C%22ISSN%22%3A%221064-8275%2C%201095-7197%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fepubs.siam.org%5C%2Fdoi%5C%2F10.1137%5C%2F100812781%22%2C%22collections%22%3A%5B%22A7A2VE5G%22%5D%2C%22dateModified%22%3A%222024-02-20T03%3A47%3A28Z%22%7D%7D%2C%7B%22key%22%3A%22DUBZCX5L%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3Eall%20the%20zeros%20of%20%26%23x1D700%3B%28k%26%23xFFFD%3B%2C%20%26%23x1D714%3B%26%23xFFFD%3B%29%20lie%20in%20the%20lower%20half%20%26%23x1D714%3B%26%23xA0%3B%20plane.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22parentItem%22%3A%22JCTI2PI7%22%2C%22itemType%22%3A%22annotation%22%2C%22annotationType%22%3A%22highlight%22%2C%22annotationText%22%3A%22all%20the%20zeros%20of%20%5Cud835%5Cudf00%28k%5Cufffd%2C%20%5Cud835%5Cudf14%5Cufffd%29%20lie%20in%20the%20lower%20half%20%5Cud835%5Cudf14%20%20plane%22%2C%22annotationComment%22%3A%22%5Cu5426%5Cu5219%5Cu4f1a%5Cu4ea7%5Cu751f%5Cu4e0d%5Cu7a33%5Cu5b9a%5Cu6027%5Cuff08%5Cu6b63%5Cu53cd%5Cu9988%5Cuff09%22%2C%22annotationColor%22%3A%22%23ffd400%22%2C%22annotationPageLabel%22%3A%2216%22%2C%22annotationSortIndex%22%3A%2200015%7C000350%7C00226%22%2C%22annotationPosition%22%3A%22%7B%5C%22pageIndex%5C%22%3A15%2C%5C%22rects%5C%22%3A%5B%5B279.065%2C425.472%2C388.206%2C439.598%5D%2C%5B51.021%2C413.472%2C153.449%2C426.808%5D%5D%7D%22%2C%22dateModified%22%3A%222024-02-17T15%3A43%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22ZPF4ZBTT%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3E%26%23x1D6FF%3B%26%23×303%3B%20NS%20%26%23x1D6FD%3B%20%28k%2C%20v%2C%20%26%23x1D714%3B%29%3D%201%20%282%26%23x1D70B%3B%293%26%23xA0%3B%20%20d3r%26%23xA0%3B%20%20%26%23x221E%3B%200%20dt%20%26%23x1D6FF%3BN%26%23x1D6FD%3B%20%28r%20%26%23×2212%3B%20vt%2C%20v%2C0%29e%26%23×2212%3Bi%28k%26%23x22C5%3Br%26%23×2212%3B%26%23x1D714%3Bt%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22parentItem%22%3A%22JCTI2PI7%22%2C%22itemType%22%3A%22annotation%22%2C%22annotationType%22%3A%22highlight%22%2C%22annotationText%22%3A%22%5Cud835%5Cudeff%5Cu0303%20NS%20%5Cud835%5Cudefd%20%28k%2C%20v%2C%20%5Cud835%5Cudf14%29%3D%201%20%282%5Cud835%5Cudf0b%293%20%20%20d3r%20%20%20%5Cu221e%200%20dt%20%5Cud835%5CudeffN%5Cud835%5Cudefd%20%28r%20%5Cu2212%20vt%2C%20v%2C0%29e%5Cu2212i%28k%5Cu22c5r%5Cu2212%5Cud835%5Cudf14t%29%22%2C%22annotationComment%22%3A%22%5Cu8fd9%5Cu91cc%5Cu5047%5Cu8bbe%5Cu4e86delta%20N%28r%2Cv%2Ct%29%3Ddelta%20N%28r-vt%2Cv%2C0%29%5Cuff0c%5Cu5373t%5Cu65f6%5Cu523b%5Cu7684%5Cu7c92%5Cu5b50%5Cu90fd%5Cu662f%5Cu4ece0%5Cu65f6%5Cu523b%5Cu76f4%5Cu7ebf%5Cu98de%5Cu6765%5Cu7684%5Cu3002%5Cu4f46%5Cu662f%5Cu6839%5Cu636e45%5Cuff0c%5Cu8fd9%5Cu91cc%5Cu597d%5Cu50cf%5Cu5c11%5Cu4e86%5Cu7b2c%5Cu4e8c%5Cu9879%5Cuff1f%5Cu539f%5Cu56e0%5Cuff1adelta%20E%5Cu5bf9%5Cu5168%5Cu7a7a%5Cu95f4%5Cu7684%5Cu79ef%5Cu5206%3D0%5Cuff0c%5Cu7136%5Cu800c%5Cu5206%5Cu5e03%5Cu51fd%5Cu6570%5Cu6ca1%5Cu6709%5Cu8fd9%5Cu4e2a%5Cu6027%5Cu8d28%5Cu3002%22%2C%22annotationColor%22%3A%22%23ffd400%22%2C%22annotationPageLabel%22%3A%2214%22%2C%22annotationSortIndex%22%3A%2200013%7C000829%7C00082%22%2C%22annotationPosition%22%3A%22%7B%5C%22pageIndex%5C%22%3A13%2C%5C%22rects%5C%22%3A%5B%5B93.32%2C572.381%2C103.641%2C583.959%5D%2C%5B98.349%2C572.166%2C109.124%2C583.03%5D%2C%5B105.021%2C569.44%2C172.358%2C586.925%5D%2C%5B158.993%2C564.741%2C217.575%2C583.191%5D%2C%5B223.073%2C583.929%2C229.557%2C590.455%5D%2C%5B217.577%2C564.184%2C221.078%2C569.856%5D%2C%5B231.722%2C570.44%2C345.986%2C583.499%5D%5D%7D%22%2C%22dateModified%22%3A%222024-02-17T15%3A36%3A41Z%22%7D%7D%2C%7B%22key%22%3A%22NRNKUUQX%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3E%26%23×2207%3B2%26%23x1D6FF%3B%26%23x1D719%3B%20%3D%26%23×2212%3B1%20%26%23x1D700%3B0%26%23xA0%3B%20%20%26%23x1D6FD%3B%20q%26%23x1D6FD%3B%26%23xA0%3B%20%20d3v%26%23xA0%3B%20%20%26%23x1D6FF%3BN%26%23x1D6FD%3B%28r%20%26%23×2212%3B%20vt%2C%20v%2C0%29%20%2B%20q%26%23x1D6FD%3B%20m%26%23x1D6FD%3B%26%23xA0%3B%20%20t%200%20dt%26%23xFFFD%3B%20%26%23×2207%3B%26%23x1D6FF%3B%26%23x1D719%3B%28r%20%26%23×2212%3B%20v%28t%20%26%23×2212%3B%20t%26%23xFFFD%3B%29%2C%20t%26%23xFFFD%3B%29%20%26%23x22C5%3B%20%26%23x1D715%3Bf%26%23x1D6FD%3B%20%28v%29%20%26%23x1D715%3Bv%26%23xA0%3B%20%20.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22parentItem%22%3A%22JCTI2PI7%22%2C%22itemType%22%3A%22annotation%22%2C%22annotationType%22%3A%22highlight%22%2C%22annotationText%22%3A%22%5Cu22072%5Cud835%5Cudeff%5Cud835%5Cudf19%20%3D%5Cu22121%20%5Cud835%5Cudf000%20%20%20%5Cud835%5Cudefd%20q%5Cud835%5Cudefd%20%20%20d3v%20%20%20%5Cud835%5CudeffN%5Cud835%5Cudefd%28r%20%5Cu2212%20vt%2C%20v%2C0%29%20%2B%20q%5Cud835%5Cudefd%20m%5Cud835%5Cudefd%20%20%20t%200%20dt%5Cufffd%20%5Cu2207%5Cud835%5Cudeff%5Cud835%5Cudf19%28r%20%5Cu2212%20v%28t%20%5Cu2212%20t%5Cufffd%29%2C%20t%5Cufffd%29%20%5Cu22c5%20%5Cud835%5Cudf15f%5Cud835%5Cudefd%20%28v%29%20%5Cud835%5Cudf15v%20%20%20.%22%2C%22annotationComment%22%3A%22%5Cu672c%5Cu8d28%5Cu4e0a%5Cu662f%5Cu7ebf%5Cu6027Vlasov%5Cu65b9%5Cu7a0b%5Cu548cPoisson%5Cu65b9%5Cu7a0b%5Cu8054%5Cu7acb%5Cuff0c%5Cu5f97%5Cu5230phi%28k%2Cw%29%5Cu7684%5Cu8fc7%5Cu7a0b%22%2C%22annotationColor%22%3A%22%23ffd400%22%2C%22annotationPageLabel%22%3A%2213%22%2C%22annotationSortIndex%22%3A%2200012%7C001105%7C00377%22%2C%22annotationPosition%22%3A%22%7B%5C%22pageIndex%5C%22%3A12%2C%5C%22rects%5C%22%3A%5B%5B112.845%2C273.427%2C163.018%2C288.331%5D%2C%5B156.09%2C265.282%2C164.433%2C276.139%5D%2C%5B167.799%2C282.256%2C180.722%2C294.349%5D%2C%5B172.308%2C263.377%2C175.76%2C269.938%5D%2C%5B182.388%2C266.301%2C220.482%2C284.579%5D%2C%5B222.15%2C287.278%2C227.231%2C299.371%5D%2C%5B227.226%2C271.828%2C295.379%2C283.141%5D%2C%5B147.872%2C240.601%2C167.696%2C258.255%5D%2C%5B158.133%2C232.016%2C178.474%2C244.194%5D%2C%5B183.972%2C252.598%2C185.919%2C258.844%5D%2C%5B178.473%2C232.769%2C181.974%2C238.44%5D%2C%5B188.211%2C240.329%2C317.81%2C258.934%5D%2C%5B300.774%2C233.957%2C310.877%2C243.329%5D%2C%5B319.008%2C254.468%2C324.089%2C266.561%5D%2C%5B324.079%2C241.605%2C326.58%2C249.707%5D%5D%7D%22%2C%22dateModified%22%3A%222024-02-17T15%3A15%3A26Z%22%7D%7D%2C%7B%22key%22%3A%22ZXMRK3CU%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3Er%26%23x1D6FC%3B%20%28t%29%3Dr%280%29%20%26%23x1D6FC%3B%20%28t%29%26%23×2212%3B%20q%26%23x1D6FC%3B%20m%26%23x1D6FC%3B%26%23xA0%3B%20%20t%200%20%28t%20%26%23×2212%3B%20t%26%23xFFFD%3B%29%26%23×2207%3B%26%23x1D6FF%3B%26%23x1D719%3B%28r%26%23x1D6FC%3B%28t%26%23xFFFD%3B%29%2C%20t%26%23xFFFD%3B%29%20dt%26%23xFFFD%3B.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22parentItem%22%3A%22JCTI2PI7%22%2C%22itemType%22%3A%22annotation%22%2C%22annotationType%22%3A%22highlight%22%2C%22annotationText%22%3A%22r%5Cud835%5Cudefc%20%28t%29%3Dr%280%29%20%5Cud835%5Cudefc%20%28t%29%5Cu2212%20q%5Cud835%5Cudefc%20m%5Cud835%5Cudefc%20%20%20t%200%20%28t%20%5Cu2212%20t%5Cufffd%29%5Cu2207%5Cud835%5Cudeff%5Cud835%5Cudf19%28r%5Cud835%5Cudefc%28t%5Cufffd%29%2C%20t%5Cufffd%29%20dt%5Cufffd.%22%2C%22annotationComment%22%3A%22%5Cu5728t%5Cu5904%5Cuff0c%5Cu800c%5Cu4e0d%5Cu662f%5Cu57280%5Cu5904%5Cuff0c%5Cu5c55%5Cu5f00%5Cu4e86%5Cu4e00%5Cu6b21%22%2C%22annotationColor%22%3A%22%23ffd400%22%2C%22annotationPageLabel%22%3A%2214%22%2C%22annotationSortIndex%22%3A%2200013%7C001001%7C00402%22%2C%22annotationPosition%22%3A%22%7B%5C%22pageIndex%5C%22%3A13%2C%5C%22rects%5C%22%3A%5B%5B122.446%2C251.18%2C165.971%2C263.959%5D%2C%5B157.807%2C250.18%2C198.367%2C269.205%5D%2C%5B188.587%2C244.18%2C208.974%2C256.357%5D%2C%5B214.471%2C264.762%2C216.417%2C271.008%5D%2C%5B208.975%2C244.933%2C212.476%2C250.605%5D%2C%5B217.045%2C251.182%2C317.331%2C263.961%5D%5D%7D%22%2C%22dateModified%22%3A%222024-02-17T14%3A57%3A42Z%22%7D%7D%2C%7B%22key%22%3A%22WUJYH9FM%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3Eand%20the%20contributions%20from%20the%20other%20parts%20of%20the%20contour%20including%20the%20horizontal%20lines%20and%20circles%20around%20the%20poles%20%26%23x1D714%3B%26%23xA0%3B%20k%20encountered%20decaying%20exponentially%20with%20t%26%23xA0%3B%20can%20be%20discarded.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22parentItem%22%3A%22JCTI2PI7%22%2C%22itemType%22%3A%22annotation%22%2C%22annotationType%22%3A%22highlight%22%2C%22annotationText%22%3A%22and%20the%20contributions%20from%20the%20other%20parts%20of%20the%20contour%20including%20the%20horizontal%20lines%20and%20circles%20around%20the%20poles%20%5Cud835%5Cudf14%20%20k%20encountered%20decaying%20exponentially%20with%20t%20%20can%20be%20discarded.%22%2C%22annotationComment%22%3A%22%5Cu56e0%5Cu4e3a%5Cu79ef%5Cu5206%5Cu8def%5Cu5f84%5Cu88ab%5Cu6362%5Cu5230%5Cu4e0b%5Cu534a%5Cu5e73%5Cu9762%5Cuff0c%5Cu76f4%5Cu7ebf%5Cu79ef%5Cu5206%5Cu4f1adecay%5Cu3002%5Cu6700%5Cu540e%5Cu53ea%5Cu5269%5Cu4e0b%5Cu6700%5Cu5927%5Cu6781%5Cu70b9%5Cu7684residue%5Cu8d21%5Cu732e%5Cu3002%5Cu8be6%5Cu89c1Waves%20in%20Plasmas%20P84%22%2C%22annotationColor%22%3A%22%23ffd400%22%2C%22annotationPageLabel%22%3A%2216%22%2C%22annotationSortIndex%22%3A%2200015%7C000711%7C00286%22%2C%22annotationPosition%22%3A%22%7B%5C%22pageIndex%5C%22%3A15%2C%5C%22rects%5C%22%3A%5B%5B339.709%2C365.472%2C388.359%2C379.588%5D%2C%5B51.019%2C353.472%2C388.181%2C365.832%5D%2C%5B51.019%2C341.472%2C128.497%2C354.899%5D%2C%5B126.116%2C341.126%2C372.106%2C354.808%5D%5D%7D%22%2C%22dateModified%22%3A%222024-02-16T14%3A46%3A40Z%22%7D%7D%2C%7B%22key%22%3A%22BKZ3GPKU%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3Ethe%20pole%20at%20%26%23x1D714%3B%26%23xFFFD%3B%20%3D%20k%26%23xFFFD%3B%20%26%23x22C5%3B%20v%26%23x1D6FC%3B%20and%20the%20poles%20%26%23x1D714%3B%26%23xFFFD%3B%20k%20%28k%20%3D%201%2C%202%2C%20%26%23x22EF%3B%29%20corresponding%20to%20the%20zeros%20of%20%26%23x1D700%3B%28k%26%23xFFFD%3B%2C%20%26%23x1D714%3B%26%23xFFFD%3B%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22parentItem%22%3A%22JCTI2PI7%22%2C%22itemType%22%3A%22annotation%22%2C%22annotationType%22%3A%22highlight%22%2C%22annotationText%22%3A%22the%20pole%20at%20%5Cud835%5Cudf14%5Cufffd%20%3D%20k%5Cufffd%20%5Cu22c5%20v%5Cud835%5Cudefc%20and%20the%20poles%20%5Cud835%5Cudf14%5Cufffd%20k%20%28k%20%3D%201%2C%202%2C%20%5Cu22ef%29%20corresponding%20to%20the%20zeros%20of%20%5Cud835%5Cudf00%28k%5Cufffd%2C%20%5Cud835%5Cudf14%5Cufffd%29%22%2C%22annotationComment%22%3A%22%5Cu6781%5Cu70b9%5Cuff1a%5Cu4e00%5Cu79cd%5Cu7531epsilon%5Cu7ed9%5Cu51fa%5Cuff0c%5Cu53e6%5Cu4e00%5Cu79cd%5Cu7531w%3Dkv%5Cu7ed9%5Cu51fa%22%2C%22annotationColor%22%3A%22%23ffd400%22%2C%22annotationPageLabel%22%3A%2216%22%2C%22annotationSortIndex%22%3A%2200015%7C000484%7C00250%22%2C%22annotationPosition%22%3A%22%7B%5C%22pageIndex%5C%22%3A15%2C%5C%22rects%5C%22%3A%5B%5B241.961%2C401.472%2C388.204%2C415.588%5D%2C%5B50.82%2C392.457%2C60.013%2C402.899%5D%2C%5B57.632%2C389.126%2C276.797%2C403.598%5D%5D%7D%22%2C%22dateModified%22%3A%222024-02-16T14%3A39%3A47Z%22%7D%7D%2C%7B%22key%22%3A%22IKWIT2DV%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Fried%20and%20Conte%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EFried%2C%20B.%20D.%20%26amp%3B%20Conte%2C%20S.%20D.%20The%20Plasma%20Dispersion%20Function.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20Plasma%20Dispersion%20Function%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Burton%20D%22%2C%22lastName%22%3A%22Fried%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Samuel%20D%22%2C%22lastName%22%3A%22Conte%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22DZI2DEM7%22%5D%2C%22dateModified%22%3A%222024-01-29T02%3A26%3A24Z%22%7D%7D%2C%7B%22key%22%3A%22EGRS7JI9%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Percival%20and%20Robinson%22%2C%22parsedDate%22%3A%221998-07-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EPercival%2C%20D.%20J.%20%26amp%3B%20Robinson%2C%20P.%20A.%20Generalized%20plasma%20dispersion%20functions.%20%3Ci%3EJournal%20of%20Mathematical%20Physics%3C%5C%2Fi%3E%20%3Cb%3E39%3C%5C%2Fb%3E%2C%203678%26%23×2013%3B3693%20%281998%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Generalized%20plasma%20dispersion%20functions%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22D.%20J.%22%2C%22lastName%22%3A%22Percival%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22P.%20A.%22%2C%22lastName%22%3A%22Robinson%22%7D%5D%2C%22abstractNote%22%3A%22Generalized%20plasma%20dispersion%20functions%20have%20recently%20arisen%20in%20the%20derivation%20of%20an%20exact%20expression%20for%20the%20quadratic%20response%20tensor%20for%20a%20plasma%20with%20constituent%20species%20having%20Maxwellian%20velocity%20distributions.%20A%20range%20of%20mathematical%20properties%20satisfied%20by%20the%20generalized%20plasma%20dispersion%20functions%20are%20derived%20here%2C%20including%20recursion%20relations%2C%20series%20expansions%2C%20and%20approximate%20analytic%20forms%2C%20including%20Pad%5Cu00e9%20approximants.%20These%20properties%20are%20of%20central%20importance%20to%20the%20application%20of%20the%20exact%20quadratic%20response%20tensor%20to%20descriptions%20of%20second-order%20processes%20in%20weak%20and%20strong%20turbulence%20theory%2C%20such%20as%20three-wave%20interactions%20in%20warm%20plasmas.%22%2C%22date%22%3A%221998-07-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1063%5C%2F1.532460%22%2C%22ISSN%22%3A%220022-2488%2C%201089-7658%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fpubs.aip.org%5C%2Fjmp%5C%2Farticle%5C%2F39%5C%2F7%5C%2F3678%5C%2F230447%5C%2FGeneralized-plasma-dispersion-functions%22%2C%22collections%22%3A%5B%22DZI2DEM7%22%5D%2C%22dateModified%22%3A%222024-01-28T06%3A44%3A45Z%22%7D%7D%2C%7B%22key%22%3A%22B7HKU9AV%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Summers%20and%20Thorne%22%2C%22parsedDate%22%3A%221991-08-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ESummers%2C%20D.%20%26amp%3B%20Thorne%2C%20R.%20M.%20The%20modified%20plasma%20dispersion%20function.%20%3Ci%3EPhysics%20of%20Fluids%20B%3A%20Plasma%20Physics%3C%5C%2Fi%3E%20%3Cb%3E3%3C%5C%2Fb%3E%2C%201835%26%23×2013%3B1847%20%281991%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20modified%20plasma%20dispersion%20function%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Danny%22%2C%22lastName%22%3A%22Summers%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20M.%22%2C%22lastName%22%3A%22Thorne%22%7D%5D%2C%22abstractNote%22%3A%22In%20the%20linear%20theory%20of%20waves%20in%20a%20hot%20plasma%20if%20the%20zeroth-order%20velocity%20distribution%20function%20is%20taken%20to%20be%20Maxwellian%2C%20then%20there%20arises%20a%20special%2C%20complex-valued%20function%20of%20a%20complex%20variable%20%5Cu03be%3Dx%2Biy%2C%20namely%20Z%28%5Cu03be%29%2C%20known%20as%20the%20plasma%20dispersion%20function.%20In%20space%20physics%20many%20particle%20distributions%20possess%20a%20high-energy%20tail%20that%20can%20be%20well%20modeled%20by%20a%20generalized%20Lorentzian%20%28or%20kappa%29%20distribution%20function%20containing%20the%20spectral%20index%20%5Cu03ba.%20In%20this%20paper%2C%20as%20a%20natural%20analog%20to%20the%20definition%20of%20Z%28%5Cu03be%29%2C%20a%20new%20special%20function%20Z%2A%5Cu03ba%28%5Cu03be%29%20is%20defined%20based%20on%20the%20kappa%20distribution%20function.%20Here%2C%20Z%2A%5Cu03ba%28%5Cu03be%29%20is%20called%20the%20modified%20plasma%20dispersion%20function.%20For%20any%20positive%20integral%20value%20of%20%5Cu03ba%2C%20Z%2A%5Cu03ba%28%5Cu03be%29%20is%20calculated%20in%20closed%20form%20as%20a%20finite%20series.%20General%20properties%2C%20including%20small-argument%20and%20large-argument%20expansions%2C%20of%20Z%2A%5Cu03ba%28%5Cu03be%29%20are%20given%2C%20and%20simple%20explicit%20forms%20are%20given%20for%20Z%2A1%28%5Cu03be%29%2C%20Z%2A2%28%5Cu03be%29%2C%20…%2C%20Z%2A6%28%5Cu03be%29.%20A%20comprehensive%20set%20of%20graphs%20of%20the%20real%20and%20imaginary%20parts%20of%20Z%2A%5Cu03ba%28%5Cu03be%29%20is%20presented.%20It%20is%20demonstrated%20how%20the%20modified%20plasma%20dispersion%20function%20approaches%20the%20plasma%20dispersion%20function%20in%20the%20limit%20as%20%5Cu03ba%5Cu2192%5Cu221e%2C%20a%20result%20to%20be%20expected%20since%20the%20%28appropriately%20defined%29%20kappa%20distribution%20function%20formally%20approaches%20the%20Maxwellian%20as%20%5Cu03ba%5Cu2192%5Cu221e.%20The%20function%20Z%2A%5Cu03ba%28%5Cu03be%29%20is%20expected%20to%20be%20instrumental%20in%20studying%20microinstabilities%20in%20plasmas%20when%20the%20particle%20distribution%20function%20is%20not%20only%20the%20standard%20generalized%20Lorentzian%2C%20but%20also%20of%20the%20Lorentzian%20type%2C%20including%20inter%5Cu2008alia%2C%20the%20loss-cone%2C%20bi-Lorentzian%2C%20and%20product%20bi-Lorentzian%20distributions.%22%2C%22date%22%3A%221991-08-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1063%5C%2F1.859653%22%2C%22ISSN%22%3A%220899-8221%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fpubs.aip.org%5C%2Fpfb%5C%2Farticle%5C%2F3%5C%2F8%5C%2F1835%5C%2F813428%5C%2FThe-modified-plasma-dispersion-function%22%2C%22collections%22%3A%5B%22DZI2DEM7%22%5D%2C%22dateModified%22%3A%222024-01-28T06%3A39%3A27Z%22%7D%7D%2C%7B%22key%22%3A%22GVDBFTSW%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ELaunchPadder-zh_CN%20%26%23×2013%3B%20%26%23x4E56%3B%26%23x773C%3B%26%23x770B%3B%26%23x4E16%3B%26%23x754C%3B.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fmolayc.com%5C%2Fblog%5C%2F2022%5C%2F04%5C%2F07%5C%2Flaunchpadder-zh_cn%5C%2F%27%3Ehttps%3A%5C%2F%5C%2Fmolayc.com%5C%2Fblog%5C%2F2022%5C%2F04%5C%2F07%5C%2Flaunchpadder-zh_cn%5C%2F%3C%5C%2Fa%3E.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22blogPost%22%2C%22title%22%3A%22LaunchPadder-zh_CN%20%5Cu2013%20%5Cu4e56%5Cu773c%5Cu770b%5Cu4e16%5Cu754c%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22blogTitle%22%3A%22%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fmolayc.com%5C%2Fblog%5C%2F2022%5C%2F04%5C%2F07%5C%2Flaunchpadder-zh_cn%5C%2F%22%2C%22language%22%3A%22zh-CN%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222024-01-01T06%3A15%3A48Z%22%7D%7D%2C%7B%22key%22%3A%2223UZQZXH%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Rutherford%22%2C%22parsedDate%22%3A%221932%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ERutherford%2C%20Lord.%20The%20Origin%20of%20the%20Gamma-Rays.%20%3Ci%3EThe%20Scientific%20Monthly%3C%5C%2Fi%3E%20%3Cb%3E34%3C%5C%2Fb%3E%2C%20483%26%23×2013%3B486%20%281932%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20Origin%20of%20the%20Gamma-Rays%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lord%22%2C%22lastName%22%3A%22Rutherford%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221932%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F15205%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-27T15%3A06%3A37Z%22%7D%7D%2C%7B%22key%22%3A%22TA3NBB35%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Wolfendale%22%2C%22parsedDate%22%3A%221991%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EWolfendale%2C%20A.%20A%20brief%20review%20of%20gamma%20ray%20astronomy.%20%3Ci%3ENuclear%20Physics%20B-Proceedings%20Supplements%3C%5C%2Fi%3E%20%3Cb%3E22%3C%5C%2Fb%3E%2C%2080%26%23×2013%3B85%20%281991%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20brief%20review%20of%20gamma%20ray%20astronomy%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Arnold%22%2C%22lastName%22%3A%22Wolfendale%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221991%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1016%5C%2F0920-5632%2891%2990008-3%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.sciencedirect.com%5C%2Fscience%5C%2Farticle%5C%2Fpii%5C%2F0920563291900083%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-27T15%3A03%3A56Z%22%7D%7D%2C%7B%22key%22%3A%222CM77TSC%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Wolfendale%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EWolfendale%2C%20A.%20A%20BRIEF%20REVIEW%20OF%20GAMMA%20RAY%20ASTRONOWi.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20BRIEF%20REVIEW%20OF%20GAMMA%20RAY%20ASTRONOWi%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Arnold%22%2C%22lastName%22%3A%22Wolfendale%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-27T15%3A03%3A31Z%22%7D%7D%2C%7B%22key%22%3A%22V4U8ZCMN%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Saxton%22%2C%22parsedDate%22%3A%221958%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ESaxton%2C%20J.%20A.%20The%20influence%20of%20atmospheric%20conditions%20on%20radar%20performance.%20%3Ci%3EThe%20Journal%20of%20Navigation%3C%5C%2Fi%3E%20%3Cb%3E11%3C%5C%2Fb%3E%2C%20290%26%23×2013%3B303%20%281958%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20influence%20of%20atmospheric%20conditions%20on%20radar%20performance%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22J.%20A.%22%2C%22lastName%22%3A%22Saxton%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221958%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1017%5C%2FS0373463300017598%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fcore%5C%2Fjournals%5C%2Fjournal-of-navigation%5C%2Farticle%5C%2Finfluence-of-atmospheric-conditions-on-radar-performance%5C%2F2D4F7F3B0F21E19B339FF10942B880D8%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A19Z%22%7D%7D%2C%7B%22key%22%3A%228EMK69KH%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Fahey%20et%20al.%22%2C%22parsedDate%22%3A%222021%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EFahey%2C%20T.%2C%20Islam%2C%20M.%2C%20Gardi%2C%20A.%20%26amp%3B%20Sabatini%2C%20R.%20Laser%20beam%20atmospheric%20propagation%20modelling%20for%20aerospace%20LIDAR%20applications.%20%3Ci%3EAtmosphere%3C%5C%2Fi%3E%20%3Cb%3E12%3C%5C%2Fb%3E%2C%20918%20%282021%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Laser%20beam%20atmospheric%20propagation%20modelling%20for%20aerospace%20LIDAR%20applications%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Fahey%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Maidul%22%2C%22lastName%22%3A%22Islam%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alessandro%22%2C%22lastName%22%3A%22Gardi%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roberto%22%2C%22lastName%22%3A%22Sabatini%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222021%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.3390%5C%2Fatmos12070918%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.mdpi.com%5C%2F2073-4433%5C%2F12%5C%2F7%5C%2F918%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A17Z%22%7D%7D%2C%7B%22key%22%3A%222THQ8DDL%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Der%20et%20al.%22%2C%22parsedDate%22%3A%221997%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EDer%2C%20S.%2C%20Redman%2C%20B.%20%26amp%3B%20Chellappa%2C%20R.%20Simulation%20of%20error%20in%20optical%20radar%20range%20measurements.%20%3Ci%3EApplied%20Optics%3C%5C%2Fi%3E%20%3Cb%3E36%3C%5C%2Fb%3E%2C%206869%26%23×2013%3B6874%20%281997%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Simulation%20of%20error%20in%20optical%20radar%20range%20measurements%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sandor%22%2C%22lastName%22%3A%22Der%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Brian%22%2C%22lastName%22%3A%22Redman%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Rama%22%2C%22lastName%22%3A%22Chellappa%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221997%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1364%5C%2FAO.36.006869%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fopg.optica.org%5C%2Fabstract.cfm%3Furi%3Dao-36-27-6869%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22PXGFK2GL%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Wu%20et%20al.%22%2C%22parsedDate%22%3A%222014%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EWu%2C%20J.%2C%20Wang%2C%20C.%20%26amp%3B%20Song%2C%20S.%20%26%23×6708%3B%26%23×7403%3B%26%23×7740%3B%26%23×9646%3B%26%23×5668%3B%26%23×5178%3B%26%23x578B%3B%26%23×6545%3B%26%23x969C%3B%26%23x6A21%3B%26%23x5F0F%3B%26%23×5206%3B%26%23×6790%3B%28Analysis%20of%20Typical%20Fault%20Modes%20of%20Lunar%20Landers%29.%20%3Ci%3EJournal%20of%20Astronautics%3C%5C%2Fi%3E%20%3Cb%3E35%3C%5C%2Fb%3E%2C%20633%26%23×2013%3B638%20%282014%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22%5Cu6708%5Cu7403%5Cu7740%5Cu9646%5Cu5668%5Cu5178%5Cu578b%5Cu6545%5Cu969c%5Cu6a21%5Cu5f0f%5Cu5206%5Cu6790%28Analysis%20of%20Typical%20Fault%20Modes%20of%20Lunar%20Landers%29%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jianyun%22%2C%22lastName%22%3A%22Wu%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Chunjie%22%2C%22lastName%22%3A%22Wang%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Shunguang%22%2C%22lastName%22%3A%22Song%22%7D%5D%2C%22abstractNote%22%3A%22%5Cu4e3a%5Cu63d0%5Cu9ad8%5Cu6708%5Cu7403%5Cu7740%5Cu9646%5Cu5668%5Cu7740%5Cu9646%5Cu53ef%5Cu9760%5Cu6027%2C%5Cu9700%5Cu8bc6%5Cu522b%5Cu6f5c%5Cu5728%5Cu7684%5Cu6545%5Cu969c%5Cu6a21%5Cu5f0f%5Cu5bf9%5Cu7a33%5Cu5b9a%5Cu6027%5Cu7740%5Cu9646%5Cu5e26%5Cu6765%5Cu7684%5Cu5f71%5Cu54cd%5Cu3002%5Cu5efa%5Cu7acb%5Cu4e86%5Cu7740%5Cu9646%5Cu5668%5Cu7684%5Cu52a8%5Cu529b%5Cu5b66%5Cu6a21%5Cu578b%2C%5Cu7ed9%5Cu51fa%5Cu4e86%5Cu7740%5Cu9646%5Cu5668%5Cu7740%5Cu9646%5Cu65f6%5Cu7684%5Cu4e03%5Cu79cd%5Cu6781%5Cu9650%5Cu5de5%5Cu51b5%2C%5Cu4f5c%5Cu4e3a%5Cu6545%5Cu969c%5Cu6a21%5Cu5f0f%5Cu5206%5Cu6790%5Cu7684%5Cu57fa%5Cu7840%3B%5Cu9488%5Cu5bf9%5Cu52a8%5Cu529b%5Cu4e0b%5Cu964d%5Cu6bb5%5Cu4e09%5Cu79cd%5Cu5178%5Cu578b%5Cu6545%5Cu969c%5Cu6a21%5Cu5f0f%2C%5Cu5373%5Cu4e3b%5Cu53d1%5Cu52a8%5Cu673a%5Cu5ef6%5Cu65f6%5Cu5173%5Cu673a%5Cu3001%5Cu50a8%5Cu7bb1%5Cu6b8b%5Cu7559%5Cu6db2%5Cu4f53%5Cu7740%5Cu9646%5Cu548c%5Cu89e6%5Cu6708%5Cu4fe1%5Cu53f7%5Cu5ef6%5Cu8fdf%5Cu53d1%5Cu51fa%2C%5Cu5efa%5Cu7acb%5Cu4e0e%5Cu5ef6%5Cu65f6%5Cu5173%5Cu673a%5Cu5bf9%5Cu5e94%5Cu7684%5Cu4e0a%5Cu629b%5Cu3001%5Cu5e73%5Cu629b%5Cu8fd0%5Cu52a8%5Cu548c%5Cu6570%5Cu5b66%5Cu5173%5Cu7cfb%2C%5Cu4e0e%5Cu6b8b%5Cu7559%5Cu6db2%5Cu4f53%5Cu7740%5Cu9646%5Cu7b49%5Cu6548%5Cu7684%5Cu5355%5Cu6446%5Cu6a21%5Cu578b%2C%5Cu65bd%5Cu52a0%5Cu89e6%5Cu6708%5Cu4fe1%5Cu53f7%5Cu5ef6%5Cu8fdf%5Cu53d1%5Cu51fa%5Cu6240%5Cu4ea7%5Cu751f%5Cu7684%5Cu63a8%5Cu529b%5Cu66f2%5Cu7ebf%2C%5Cu5229%5Cu7528Adams%5Cu8f6f%5Cu4ef6%5Cu8fdb%5Cu884c%5Cu52a8%5Cu529b%5Cu5b66%5Cu4eff%5Cu771f%3B%5Cu7ed3%5Cu679c%5Cu8868%5Cu660e%5Cu50a8%5Cu7bb1%5Cu6b8b%5Cu7559%5Cu6db2%5Cu4f53%5Cu7740%5Cu9646%5Cu5f71%5Cu54cd%5Cu8f83%5Cu5c0f%2C%5Cu53e6%5Cu5916%5Cu4e24%5Cu79cd%5Cu6545%5Cu969c%5Cu6a21%5Cu5f0f%5Cu4f7f%5Cu7740%5Cu9646%5Cu65f6%5Cu6297%5Cu503e%5Cu5012%5Cu6027%5Cu80fd%5Cu548c%5Cu7f13%5Cu51b2%5Cu6027%5Cu80fd%5Cu6076%5Cu5316%2C%5Cu589e%5Cu52a0%5Cu7740%5Cu9646%5Cu4e0d%5Cu7a33%5Cu5b9a%5Cu6027%5Cu3002%22%2C%22date%22%3A%222014%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22N33B7459%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Wang%20and%20Richardson%22%2C%22parsedDate%22%3A%222015%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EWang%2C%20H.%20%26amp%3B%20Richardson%2C%20M.%20I.%20The%20origin%2C%20evolution%2C%20and%20trajectory%20of%20large%20dust%20storms%20on%20Mars%20during%20Mars%20years%2024%26%23×2013%3B30%20%281999%26%23×2013%3B2011%29.%20%3Ci%3EIcarus%3C%5C%2Fi%3E%20%3Cb%3E251%3C%5C%2Fb%3E%2C%20112%26%23×2013%3B127%20%282015%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20origin%2C%20evolution%2C%20and%20trajectory%20of%20large%20dust%20storms%20on%20Mars%20during%20Mars%20years%2024%5Cu201330%20%281999%5Cu20132011%29%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Huiqun%22%2C%22lastName%22%3A%22Wang%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Mark%20I.%22%2C%22lastName%22%3A%22Richardson%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222015%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.icarus.2013.10.033%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.sciencedirect.com%5C%2Fscience%5C%2Farticle%5C%2Fpii%5C%2FS0019103513004624%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22Q9S68PG6%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22%5Cu5b59%5Cu5360%5Cu6d77%20and%20%5Cu7f57%5Cu514b%22%2C%22parsedDate%22%3A%222011%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3E%26%23x5B59%3B%26%23×5360%3B%26%23x6D77%3B%20%26amp%3B%20%26%23x7F57%3B%26%23x514B%3B.%20%26%23x201C%3B%26%23x795E%3B%26%23x821F%3B%26%23x516B%3B%26%23x53F7%3B%26%23x201D%3B%20%26%23x98DE%3B%26%23×8239%3B%20%26%23x3B3%3B%20%26%23x6E90%3B%26%23x9AD8%3B%26%23x5EA6%3B%26%23x63A7%3B%26%23×5236%3B%26%23x88C5%3B%26%23x7F6E%3B%26%23x5B89%3B%26%23x88C5%3B%26%23x5DE5%3B%26%23×5177%3B%26%23x548C%3B%26%23x65B9%3B%26%23x6CD5%3B%26%23×7684%3B%26%23×6539%3B%26%23x8FDB%3B.%20%26%23x822A%3B%26%23×5929%3B%26%23×5668%3B%26%23x73AF%3B%26%23×5883%3B%26%23x5DE5%3B%26%23x7A0B%3B%20%3Cb%3E28%3C%5C%2Fb%3E%2C%20650%26%23×2013%3B651%20%282011%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22%5Cu201c%5Cu795e%5Cu821f%5Cu516b%5Cu53f7%5Cu201d%20%5Cu98de%5Cu8239%20%5Cu03b3%20%5Cu6e90%5Cu9ad8%5Cu5ea6%5Cu63a7%5Cu5236%5Cu88c5%5Cu7f6e%5Cu5b89%5Cu88c5%5Cu5de5%5Cu5177%5Cu548c%5Cu65b9%5Cu6cd5%5Cu7684%5Cu6539%5Cu8fdb%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22name%22%3A%22%5Cu5b59%5Cu5360%5Cu6d77%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22name%22%3A%22%5Cu7f57%5Cu514b%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222011%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fwww.cqvip.com%5C%2Fqk%5C%2F89474x%5C%2F201106%5C%2F40655753.html%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22KDHSCSAD%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22van%20Eijk%20and%20Stein%22%2C%22parsedDate%22%3A%222017%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3Evan%20Eijk%2C%20A.%20M.%20%26amp%3B%20Stein%2C%20K.%20Atmospheric%20and%20laser%20propagation.%20%3Ci%3ETechnologies%20for%20Optical%20Countermeasures%20XIV%3C%5C%2Fi%3E%20%3Cb%3E10435%3C%5C%2Fb%3E%2C%2042%26%23×2013%3B51%20%282017%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Atmospheric%20and%20laser%20propagation%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alexander%20MJ%22%2C%22lastName%22%3A%22van%20Eijk%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Karin%22%2C%22lastName%22%3A%22Stein%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222017%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.spiedigitallibrary.org%5C%2Fconference-proceedings-of-spie%5C%2F10435%5C%2F104350E%5C%2FAtmospheric-and-laser-propagation%5C%2F10.1117%5C%2F12.2275865.short%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22DPIN5N5W%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22%5Cu5f20%5Cu6960%20et%20al.%22%2C%22parsedDate%22%3A%222014%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3E%26%23x5F20%3B%26%23×6960%3B%2C%20%26%23×5434%3B%26%23x4E16%3B%26%23x901A%3B%20%26amp%3B%20%26%23x6C88%3B%26%23x8D85%3B.%20%26%23x3B3%3B%26%23x6E90%3B%26%23x8F90%3B%26%23x5C04%3B%26%23x89D2%3B%26%23x5EA6%3B%26%23x5BF9%3B%26%23×5149%3B%26%23x5B50%3B%26%23x9AD8%3B%26%23x5EA6%3B%26%23x8BA1%3B%26%23×6027%3B%26%23x80FD%3B%26%23×7684%3B%26%23x5F71%3B%26%23x54CD%3B%26%23×5206%3B%26%23×6790%3B%28Analysis%20of%20Effect%20of%20%26%23x3B3%3B%20Radiation%20Angle%20on%20the%20Photons%20Altimeter%29.%20%26%23x822A%3B%26%23×5929%3B%26%23x8FD4%3B%26%23x56DE%3B%26%23x4E0E%3B%26%23×9065%3B%26%23x611F%3B%20%3Cb%3E35%3C%5C%2Fb%3E%2C%2037%26%23×2013%3B41%20%282014%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22%5Cu03b3%5Cu6e90%5Cu8f90%5Cu5c04%5Cu89d2%5Cu5ea6%5Cu5bf9%5Cu5149%5Cu5b50%5Cu9ad8%5Cu5ea6%5Cu8ba1%5Cu6027%5Cu80fd%5Cu7684%5Cu5f71%5Cu54cd%5Cu5206%5Cu6790%28Analysis%20of%20Effect%20of%20%5Cu03b3%20Radiation%20Angle%20on%20the%20Photons%20Altimeter%29%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%22%2C%22lastName%22%3A%22%5Cu5f20%5Cu6960%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%22%2C%22lastName%22%3A%22%5Cu5434%5Cu4e16%5Cu901a%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%22%2C%22lastName%22%3A%22%5Cu6c88%5Cu8d85%22%7D%5D%2C%22abstractNote%22%3A%22%5Cu4e3a%5Cu4e86%5Cu7814%5Cu7a76%5Cu5206%5Cu6790%5Cu6708%5Cu7403%5Cu73af%5Cu5883%5Cu4e0b%5Cu03b3%5Cu5149%5Cu5b50%5Cu9ad8%5Cu5ea6%5Cu8ba1%5Cu6e90%5Cu8f90%5Cu5c04%5Cu89d2%5Cu5ea6%5Cu5bf9%5Cu5176%5Cu6027%5Cu80fd%5Cu7684%5Cu5f71%5Cu54cd%2C%5Cu6587%5Cu7ae0%5Cu5efa%5Cu7acb%5Cu4e86%5Cu6708%5Cu7403%5Cu7740%5Cu9646%5Cu5668%5Cu7b80%5Cu5316%5Cu6a21%5Cu578b%2C%5Cu5229%5Cu7528%5Cu57fa%5Cu4e8e%5Cu8499%5Cu7279%5Cu5361%5Cu7f57%5Cu65b9%5Cu6cd5%5Cu7684%5Cu7c92%5Cu5b50%5Cu8f93%5Cu8fd0%5Cu7a0b%5Cu5e8f%28MCNP%29%5Cu8f6f%5Cu4ef6%5Cu4eff%5Cu771f%5Cu8ba1%5Cu7b97%5Cu4e86%5Cu63a5%5Cu6536%5Cu5904%5Cu7406%5Cu5668%5Cu6355%5Cu83b7%5Cu7684%5Cu5149%5Cu5b50%5Cu8ba1%5Cu6570%5Cu968f%5Cu03b3%5Cu6e90%5Cu8f90%5Cu5c04%5Cu89d2%5Cu5ea6%5Cu7684%5Cu53d8%5Cu5316%5Cu89c4%5Cu5f8b%5Cu3002%5Cu4eff%5Cu771f%5Cu7ed3%5Cu679c%5Cu8868%5Cu660e%3A%5Cu8f90%5Cu5c04%5Cu89d2%5Cu5ea6%5Cu5c0f%5Cu4e8e%5Cu4e00%5Cu5b9a%5Cu503c%5Cu65f6%2C%5Cu5149%5Cu5b50%5Cu8ba1%5Cu6570%5Cu968f%5Cu7740%5Cu8f90%5Cu5c04%5Cu89d2%5Cu5ea6%5Cu7684%5Cu589e%5Cu5927%5Cu8fd1%5Cu4f3c%5Cu5448%5Cu7ebf%5Cu6027%5Cu589e%5Cu957f%3B%5Cu5f53%5Cu03b3%5Cu6e90%5Cu8f90%5Cu5c04%5Cu89d2%5Cu5ea6%5Cu589e%5Cu5927%5Cu5230%5Cu4e00%5Cu5b9a%5Cu503c%5Cu65f6%2C%5Cu5149%5Cu5b50%5Cu8ba1%5Cu6570%5Cu57fa%5Cu672c%5Cu4e0d%5Cu518d%5Cu6709%5Cu53d8%5Cu5316%5Cu3002%5Cu6587%5Cu7ae0%5Cu7684%5Cu5206%5Cu6790%5Cu65b9%5Cu6cd5%5Cu548c%5Cu7ed3%5Cu679c%5Cu53ef%5Cu4ee5%5Cu4e3a%5Cu5408%5Cu7406%5Cu786e%5Cu5b9a%5Cu03b3%5Cu5149%5Cu5b50%5Cu9ad8%5Cu5ea6%5Cu8ba1%5Cu6e90%5Cu8f90%5Cu5c04%5Cu89d2%5Cu5ea6%5Cu63d0%5Cu4f9b%5Cu8bbe%5Cu8ba1%5Cu53c2%5Cu8003%5Cu3002%22%2C%22date%22%3A%222014%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fkns.cnki.net%5C%2Fkcms2%5C%2Farticle%5C%2Fabstract%3Fv%3DlWc4gvQ5J153LQlMB0IoWlYfIVu_1tXPzqBGqNfu9JTaJ0jMsZ_kBDETNKWj9L4UDaZv6-hpIxs_Z7Ov4y_R-tYR9VPfDLVazDKj4yCU5dMVsTMGVAeCr_VDQIIw5Xa7JXwxxmd0UHWOdFPwU2A-iw%3D%3D%26uniplatform%3DNZKPT%26language%3DCHS%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22DVB5DNQZ%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22McLeod%20et%20al.%22%2C%22parsedDate%22%3A%222020%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EMcLeod%2C%20R.%20R.%2C%20Villalobos%2C%20I.%20P.%2C%20Tomita%2C%20Y.%20%26amp%3B%20Sheridan%2C%20J.%20T.%20Photosensitive%20Materials%20and%20their%20Applications.%20in%20%3Ci%3EProc.%20of%20SPIE%20Vol%3C%5C%2Fi%3E%20vol.%2011367%201136701%26%23×2013%3B1%20%282020%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22conferencePaper%22%2C%22title%22%3A%22Photosensitive%20Materials%20and%20their%20Applications%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robert%20R.%22%2C%22lastName%22%3A%22McLeod%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Inmaculada%20Pascual%22%2C%22lastName%22%3A%22Villalobos%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Yasuo%22%2C%22lastName%22%3A%22Tomita%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20T.%22%2C%22lastName%22%3A%22Sheridan%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222020%22%2C%22proceedingsTitle%22%3A%22Proc.%20of%20SPIE%20Vol%22%2C%22conferenceName%22%3A%22%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.spiedigitallibrary.org%5C%2Fproceedings%5C%2FDownload%3FurlId%3D10.1117%252F12.2571803%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A16Z%22%7D%7D%2C%7B%22key%22%3A%229ERX3A76%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Leslie%20and%20Youmans%22%2C%22parsedDate%22%3A%221995%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ELeslie%2C%20D.%20H.%20%26amp%3B%20Youmans%2C%20D.%20G.%20Atmospheric%20effects%20on%20eye-safe%20airborne%20laser%20radar.%20in%20%3Ci%3EBeam%20Control%2C%20Diagnostics%2C%20Standards%2C%20and%20Propagation%3C%5C%2Fi%3E%20vol.%202375%2017%26%23×2013%3B29%20%28SPIE%2C%201995%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22conferencePaper%22%2C%22title%22%3A%22Atmospheric%20effects%20on%20eye-safe%20airborne%20laser%20radar%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Daniel%20H.%22%2C%22lastName%22%3A%22Leslie%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Douglas%20G.%22%2C%22lastName%22%3A%22Youmans%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221995%22%2C%22proceedingsTitle%22%3A%22Beam%20Control%2C%20Diagnostics%2C%20Standards%2C%20and%20Propagation%22%2C%22conferenceName%22%3A%22%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1117%5C%2F12.206988%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.spiedigitallibrary.org%5C%2Fconference-proceedings-of-spie%5C%2F2375%5C%2F0000%5C%2FAtmospheric-effects-on-eye-safe-airborne-laser-radar%5C%2F10.1117%5C%2F12.206988.short%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-26T06%3A14%3A16Z%22%7D%7D%2C%7B%22key%22%3A%22924ENH3Z%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22parsedDate%22%3A%222023-12-10%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EGamma%20Ray%20Ranging%20for%20Spacecraft%20Landings%20%26%23×2013%3B%20Keheng%26%23×2019%3Bs%20Physics%20Playground.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Fkehengphysics.site%5C%2Fgamma-ray-ranging%5C%2F%27%3Ehttp%3A%5C%2F%5C%2Fkehengphysics.site%5C%2Fgamma-ray-ranging%5C%2F%3C%5C%2Fa%3E%20%282023%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22blogPost%22%2C%22title%22%3A%22Gamma%20Ray%20Ranging%20for%20Spacecraft%20Landings%20%5Cu2013%20Keheng%27s%20Physics%20Playground%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22blogTitle%22%3A%22%22%2C%22date%22%3A%222023-12-10%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fkehengphysics.site%5C%2Fgamma-ray-ranging%5C%2F%22%2C%22language%22%3A%22en-US%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-25T02%3A34%3A48Z%22%7D%7D%2C%7B%22key%22%3A%22YALTLAAZ%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Dumont%22%2C%22parsedDate%22%3A%222007-11-14%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EDumont%2C%20R.%20%3Ci%3EWaves%20in%20Plasmas%3C%5C%2Fi%3E.%20%282007%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22Waves%20in%20Plasmas%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22R.%22%2C%22lastName%22%3A%22Dumont%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22November%2014%2C%202007%22%2C%22language%22%3A%22%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22DZI2DEM7%22%5D%2C%22dateModified%22%3A%222023-12-24T07%3A18%3A10Z%22%7D%7D%2C%7B%22key%22%3A%225I4XUHSI%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Bobylev%20and%20Nanbu%22%2C%22parsedDate%22%3A%222000-04-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EBobylev%2C%20A.%20V.%20%26amp%3B%20Nanbu%2C%20K.%20Theory%20of%20collision%20algorithms%20for%20gases%20and%20plasmas%20based%20on%20the%20Boltzmann%20equation%20and%20the%20Landau-Fokker-Planck%20equation.%20%3Ci%3EPhys.%20Rev.%20E%3C%5C%2Fi%3E%20%3Cb%3E61%3C%5C%2Fb%3E%2C%204576%26%23×2013%3B4586%20%282000%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Theory%20of%20collision%20algorithms%20for%20gases%20and%20plasmas%20based%20on%20the%20Boltzmann%20equation%20and%20the%20Landau-Fokker-Planck%20equation%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22A.%20V.%22%2C%22lastName%22%3A%22Bobylev%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22K.%22%2C%22lastName%22%3A%22Nanbu%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222000-4-1%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1103%5C%2FPhysRevE.61.4576%22%2C%22ISSN%22%3A%221063-651X%2C%201095-3787%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flink.aps.org%5C%2Fdoi%5C%2F10.1103%5C%2FPhysRevE.61.4576%22%2C%22collections%22%3A%5B%22VIQQ54CQ%22%5D%2C%22dateModified%22%3A%222023-12-24T04%3A45%3A00Z%22%7D%7D%2C%7B%22key%22%3A%22WQQ3KQLS%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ECoulomb%20collisions%20in%20plasma%20can%20be%20treated%20as%20successive%20binary%20collisions%20%405%23.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22parentItem%22%3A%225VPD7D3B%22%2C%22itemType%22%3A%22annotation%22%2C%22annotationType%22%3A%22highlight%22%2C%22annotationText%22%3A%22Coulomb%20collisions%20in%20plasma%20can%20be%20treated%20as%20successive%20binary%20collisions%20%405%23%22%2C%22annotationComment%22%3A%22%22%2C%22annotationColor%22%3A%22%23ffd400%22%2C%22annotationPageLabel%22%3A%224642%22%2C%22annotationSortIndex%22%3A%2200000%7C004025%7C00592%22%2C%22annotationPosition%22%3A%22%7B%5C%22pageIndex%5C%22%3A0%2C%5C%22rects%5C%22%3A%5B%5B326.954%2C189.457%2C560.469%2C199.434%5D%2C%5B314.98%2C177.982%2C397.768%2C187.96%5D%5D%7D%22%2C%22dateModified%22%3A%222023-12-24T04%3A44%3A09Z%22%7D%7D%2C%7B%22key%22%3A%22BHKEXIC9%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Cohen%20et%20al.%22%2C%22parsedDate%22%3A%221950-10-15%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ECohen%2C%20R.%20S.%2C%20Spitzer%2C%20L.%20%26amp%3B%20Routly%2C%20P.%20McR.%20The%20Electrical%20Conductivity%20of%20an%20Ionized%20Gas.%20%3Ci%3EPhys.%20Rev.%3C%5C%2Fi%3E%20%3Cb%3E80%3C%5C%2Fb%3E%2C%20230%26%23×2013%3B238%20%281950%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20Electrical%20Conductivity%20of%20an%20Ionized%20Gas%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robert%20S.%22%2C%22lastName%22%3A%22Cohen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lyman%22%2C%22lastName%22%3A%22Spitzer%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Paul%20McR.%22%2C%22lastName%22%3A%22Routly%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221950-10-15%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1103%5C%2FPhysRev.80.230%22%2C%22ISSN%22%3A%220031-899X%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flink.aps.org%5C%2Fdoi%5C%2F10.1103%5C%2FPhysRev.80.230%22%2C%22collections%22%3A%5B%22VIQQ54CQ%22%5D%2C%22dateModified%22%3A%222023-12-24T04%3A31%3A30Z%22%7D%7D%2C%7B%22key%22%3A%22VVAWSPFB%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Doner%20et%20al.%22%2C%22parsedDate%22%3A%222021%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EDoner%2C%20A.%2C%20Hor%26%23xE1%3Bnyi%2C%20M.%2C%20Faller%2C%20J.%2C%20Fontanese%2C%20J.%20%26amp%3B%20Munsat%2C%20T.%20Restoring%20light%20transmission%20of%20dusty%20glass%20surfaces%20on%20the%20Moon.%20%3Ci%3EAdvances%20in%20Space%20Research%3C%5C%2Fi%3E%20%3Cb%3E68%3C%5C%2Fb%3E%2C%204050%26%23×2013%3B4055%20%282021%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Restoring%20light%20transmission%20of%20dusty%20glass%20surfaces%20on%20the%20Moon%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22A.%22%2C%22lastName%22%3A%22Doner%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22M.%22%2C%22lastName%22%3A%22Hor%5Cu00e1nyi%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22J.%22%2C%22lastName%22%3A%22Faller%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22J.%22%2C%22lastName%22%3A%22Fontanese%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22T.%22%2C%22lastName%22%3A%22Munsat%22%7D%5D%2C%22abstractNote%22%3A%22The%20Lunar%20Laser%20Ranging%20Retro-re%5Cufb02ectors%20%28LRR%29%20allow%20for%20the%20precise%20measurement%20of%20the%20travel%20time%20of%20laser%20pulses%20from%20the%20Earth%20to%20the%20lunar%20surface%20and%20back.%20Dust%20accumulation%20on%20the%20LRRs%20scatters%20the%20re%5Cufb02ected%20light%20used%20for%20laser%20interferometry%20measurements%20leading%20to%20a%20reduction%20in%20the%20return%20signal%20amplitude%20by%20a%20factor%20of%20%5Cu201910.%20We%20report%20on%20a%20series%20of%20experiments%20utilizing%20a%20method%20of%20an%20iterative%20application%20and%20removal%20of%20an%20acrylic%20adhesive%20kapton%20tape%20to%20remove%20lunar%20dust%20simulant%20from%20a%20glass%20substrate.%20The%20e%5Cufb00ectiveness%20of%20adhesive%20tape%20was%20determined%20by%20measuring%20the%20transmission%20of%20an%20expanded%20laser%20beam%20through%20a%20glass%20substrate%20with%20a%20dusted%20surface.%20Calibration%20data%20was%20obtained%20before%20the%20glass%20was%20exposed%20to%20any%20dust%2C%20and%20light%20transmission%20was%20measured%20after%20each%20iteration%20of%20adhesive%20removal%20using%20a%20power%20meter.%20The%20procedure%20was%20repeated%20using%20heavy%20gloves%20while%20keeping%20the%20glass%20substrate%20at%20120%20C%20to%20simulate%20the%20temperature%20conditions%20of%20a%20lunar%20day%20on%20the%20surface.%20A%20third%20test%20was%20conducted%20at%20room%20temperature%20in%20high-vacuum%20to%20ensure%20functionality%20in%20the%20lunar%20environment.%20These%20experiments%20show%20that%20glass%20substrates%20can%20be%20restored%20to%2098%20%5Cu00c6%202%20%25%20of%20their%20original%20transmission%20using%20the%20adhesive%20tape%20method.%20Therefore%20the%20light%20that%20travels%20into%20and%20out%20of%20the%20quartz%20surface%20of%20the%20LLRs%20can%20be%20restored%20up%20to%2096%20%5Cu00c6%204%20%25%20of%20their%20initial%20transmission.%22%2C%22date%22%3A%2211%5C%2F2021%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.asr.2021.07.020%22%2C%22ISSN%22%3A%2202731177%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0273117721005901%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T16%3A58%3A53Z%22%7D%7D%2C%7B%22key%22%3A%22CKNXM3ZM%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Zhao%20et%20al.%22%2C%22parsedDate%22%3A%222019-01-24%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EZhao%2C%20J.%2C%20Du%2C%20X.%2C%20Song%2C%20Y.%2C%20Zhu%2C%20C.%20%26amp%3B%20Chen%2C%20P.%20Study%20on%20the%20influence%20of%20aerosol%20macroscopic%20characteristics%20on%20backscattering%20signals.%20in%20%3Ci%3EThird%20International%20Conference%20on%20Photonics%20and%20Optical%20Engineering%3C%5C%2Fi%3E%20%28ed.%20Tian%2C%20A.%29%20103%20%28SPIE%2C%20Xi%26%23×2019%3Ban%2C%20China%2C%202019%29.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27http%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1117%5C%2F12.2522031%27%3Ehttp%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1117%5C%2F12.2522031%3C%5C%2Fa%3E.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22conferencePaper%22%2C%22title%22%3A%22Study%20on%20the%20influence%20of%20aerosol%20macroscopic%20characteristics%20on%20backscattering%20signals%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jiguang%22%2C%22lastName%22%3A%22Zhao%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Xiaoping%22%2C%22lastName%22%3A%22Du%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Yishuo%22%2C%22lastName%22%3A%22Song%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Changming%22%2C%22lastName%22%3A%22Zhu%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Peng%22%2C%22lastName%22%3A%22Chen%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Ailing%22%2C%22lastName%22%3A%22Tian%22%7D%5D%2C%22abstractNote%22%3A%22Aerosols%20such%20as%20fog%20and%20dust%20interfere%20with%20the%20backscattering%20of%20laser%20proximity%20detection%2C%20which%20severely%20limits%20its%20application%20range.%20In%20order%20to%20achieve%20target%20recognition%20under%20aerosol%20interference%20conditions%2C%20the%20study%20of%20backscattering%20law%20is%20carried%20out.%20Based%20on%20Monte%20Carlo%20simulation%20method%2C%20the%20model%20of%20lidar%20interaction%20with%20aerosol%20is%20established%2C%20and%20the%20time%20domain%20characteristics%20of%20backscattering%20of%20laser%20radar%20are%20simulated.%20The%20peak%20intensity%2C%20signal%20delay%20and%20waveform%20broadening%20of%20backscattering%20echoes%20under%20different%20extinction%20coefficient%20%28visibility%29%2C%20scattering%20coefficient%20and%20absorption%20coefficient%20were%20studied.%20The%20conclusions%20obtained%20from%20the%20study%20have%20certain%20reference%20significance%20for%20understanding%20the%20backscattering%20effect%20of%20aerosol%20particles%2C%20and%20also%20have%20certain%20significance%20for%20the%20subsequent%20research%20of%20anti-aerosol%20interference%20of%20laser%20detection.%22%2C%22date%22%3A%222019-1-24%22%2C%22proceedingsTitle%22%3A%22Third%20International%20Conference%20on%20Photonics%20and%20Optical%20Engineering%22%2C%22conferenceName%22%3A%22The%20International%20Conference%20on%20Photonics%20and%20Optical%20Engineering%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1117%5C%2F12.2522031%22%2C%22ISBN%22%3A%22978-1-5106-2779-6%20978-1-5106-2780-2%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.spiedigitallibrary.org%5C%2Fconference-proceedings-of-spie%5C%2F11052%5C%2F2522031%5C%2FStudy-on-the-influence-of-aerosol-macroscopic-characteristics-on-backscattering%5C%2F10.1117%5C%2F12.2522031.full%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T16%3A36%3A09Z%22%7D%7D%2C%7B%22key%22%3A%22LIGZJCRF%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Stein%20et%20al.%22%2C%22parsedDate%22%3A%222014-10-03%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EStein%2C%20K.%2C%20Gladysz%2C%20S.%2C%20Seiffer%2C%20D.%20%26amp%3B%20Zepp%2C%20A.%20Atmospheric%20limitations%20on%20the%20performance%20of%20electro-optical%20systems%3A%20a%20brief%20overview.%20in%20%28eds.%20Van%20Eijk%2C%20A.%20M.%20J.%2C%20Davis%2C%20C.%20C.%20%26amp%3B%20Hammel%2C%20S.%20M.%29%2092240U%20%28San%20Diego%2C%20California%2C%20United%20States%2C%202014%29.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27http%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1117%5C%2F12.2064631%27%3Ehttp%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1117%5C%2F12.2064631%3C%5C%2Fa%3E.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22conferencePaper%22%2C%22title%22%3A%22Atmospheric%20limitations%20on%20the%20performance%20of%20electro-optical%20systems%3A%20a%20brief%20overview%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Alexander%20M.%20J.%22%2C%22lastName%22%3A%22Van%20Eijk%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Christopher%20C.%22%2C%22lastName%22%3A%22Davis%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Stephen%20M.%22%2C%22lastName%22%3A%22Hammel%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Karin%22%2C%22lastName%22%3A%22Stein%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Szymon%22%2C%22lastName%22%3A%22Gladysz%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Dirk%22%2C%22lastName%22%3A%22Seiffer%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Andreas%22%2C%22lastName%22%3A%22Zepp%22%7D%5D%2C%22abstractNote%22%3A%22Atmospheric%20effects%20limit%20the%20performance%20of%20any%20electro-optical%20%28EO%29%20system.%20Tasks%20such%20as%20laser%20communications%20or%20horizontal-path%20imaging%20for%20long-range%20surveillance%20are%20highly%20affected%20by%20environmental%20effects.%20In%20the%20majority%20of%20cases%2C%20effects%20like%20turbulence%20impose%20a%20fundamental%20limitation%20to%20the%20capability%20of%20EO%20systems.%20In%20this%20paper%2C%20we%20give%20an%20overview%20of%20the%20limiting%20factors%20and%20we%20will%20show%20possibilities%20for%20restoration%20of%20images%20degraded%20by%20atmosphere.%22%2C%22date%22%3A%222014-10-3%22%2C%22proceedingsTitle%22%3A%22%22%2C%22conferenceName%22%3A%22SPIE%20Optical%20Engineering%20%2B%20Applications%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1117%5C%2F12.2064631%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fproceedings.spiedigitallibrary.org%5C%2Fproceeding.aspx%3Fdoi%3D10.1117%5C%2F12.2064631%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T16%3A33%3A47Z%22%7D%7D%2C%7B%22key%22%3A%22A8FB3XYX%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Cain%22%2C%22parsedDate%22%3A%222010%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ECain%2C%20J.%20R.%20Lunar%20dust%3A%20The%20Hazard%20and%20Astronaut%20Exposure%20Risks.%20%3Ci%3EEarth%20Moon%20Planets%3C%5C%2Fi%3E%20%3Cb%3E107%3C%5C%2Fb%3E%2C%20107%26%23×2013%3B125%20%282010%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Lunar%20dust%3A%20The%20Hazard%20and%20Astronaut%20Exposure%20Risks%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Cain%22%7D%5D%2C%22abstractNote%22%3A%22This%20paper%20reviews%20the%20characterisation%20of%20lunar%20dust%20or%20regolith%2C%20the%20toxicity%20of%20the%20dust%20and%20associated%20health%20effects%2C%20the%20techniques%20for%20assessing%20the%20health%20risks%20from%20dust%20exposure%20and%20describes%20the%20measures%20used%20or%20being%20developed%20to%20mitigate%20exposure.%20Lunar%20dust%20is%20formed%20from%20micrometeorite%20impacts%20onto%20the%20Moon%5Cu2019s%20surface.%20The%20hypervelocity%20impacts%20result%20in%20communition%20and%20the%20formation%20of%20sharp%20and%20clingy%20agglutinates.%20The%20dust%20particles%20vary%20in%20size%20with%20the%20smallest%20being%20less%20than%2010%20lm.%20If%20the%20chemical%20reactive%20particles%20are%20deposited%20in%20the%20lungs%2C%20they%20may%20cause%20respiratory%20disease.%20During%20lunar%20exploration%2C%20the%20astronaut%5Cu2019s%20spacesuits%20will%20become%20contaminated%20with%20lunar%20dust.%20The%20dust%20will%20be%20released%20into%20the%20atmosphere%20when%20the%20suits%20are%20removed.%20The%20exposure%20risks%20to%20health%20will%20need%20to%20be%20assessed%20by%20relating%20to%20a%20permissible%20exposure%20limit.%20During%20the%20Apollo%20missions%2C%20the%20astronauts%20were%20exposed%20to%20lunar%20dust.%20Acute%20health%20effects%20from%20dust%20inhalation%20exposure%20included%20sore%20throat%2C%20sneezing%20and%20coughing.%20Long-term%20exposure%20to%20the%20dust%20may%20cause%20a%20more%20serious%20respiratory%20disease%20similar%20to%20silicosis.%20On%20future%20missions%20the%20methods%20used%20to%20mitigate%20exposure%20will%20include%20providing%20high%20air%20recirculation%20rates%20in%20the%20airlock%2C%20the%20use%20of%20a%20%5Cu2018%5Cu2018Double%20Shell%20Spacesuit%5Cu2019%5Cu2019%20so%20that%20contaminated%20spacesuits%20are%20removed%20before%20entering%20the%20airlock%2C%20the%20use%20of%20dust%20shields%20to%20prevent%20dust%20accumulating%20on%20surfaces%2C%20the%20use%20of%20high%20gradient%20magnetic%20separation%20to%20remove%20surface%20dust%20and%20the%20use%20of%20solar%20%5Cufb02ux%20to%20sinter%20and%20melt%20the%20regolith%20around%20the%20spacecraft.%22%2C%22date%22%3A%2212%5C%2F2010%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs11038-010-9365-0%22%2C%22ISSN%22%3A%220167-9295%2C%201573-0794%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs11038-010-9365-0%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T15%3A36%3A41Z%22%7D%7D%2C%7B%22key%22%3A%22CUFKV4PS%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ranvier%20et%20al.%22%2C%22parsedDate%22%3A%222020-03-23%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ERanvier%2C%20S.%2C%20Hess%2C%20S.%2C%20Mateo%20Velez%2C%20J.-C.%2C%20Alvaro%20Sanchez%2C%20A.%20%26amp%3B%20De%20Keyser%2C%20J.%20%3Ci%3EDUSTER%3A%20A%20Multi-Sensor%20Instrument%20to%20Study%20Dust%20Transport%20and%20Electrostatic%20Removal%20for%20Exploration%20Missions%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fmeetingorganizer.copernicus.org%5C%2FEGU2020%5C%2FEGU2020-21638.html%27%3Ehttps%3A%5C%2F%5C%2Fmeetingorganizer.copernicus.org%5C%2FEGU2020%5C%2FEGU2020-21638.html%3C%5C%2Fa%3E%20%282020%29%20doi%3A10.5194%5C%2Fegusphere-egu2020-21638.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22report%22%2C%22title%22%3A%22DUSTER%3A%20a%20multi-sensor%20instrument%20to%20study%20dust%20transport%20and%20electrostatic%20removal%20for%20exploration%20missions%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sylvain%22%2C%22lastName%22%3A%22Ranvier%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sebastien%22%2C%22lastName%22%3A%22Hess%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jean-Charles%22%2C%22lastName%22%3A%22Mateo%20Velez%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Angel%22%2C%22lastName%22%3A%22Alvaro%20Sanchez%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Johan%22%2C%22lastName%22%3A%22De%20Keyser%22%7D%5D%2C%22abstractNote%22%3A%22%26lt%3Bp%26gt%3BOne%20major%20environmental%20constraint%20during%20exploration%20missions%20is%20the%20presence%20of%20charged%20dust-like%20particles%2C%20which%20are%20present%20on%20the%20Moon%2C%20Mars%2C%20comets%20and%20asteroids.%20From%20an%20analysis%20of%20the%20effects%20of%20lunar%20dust%20on%20Extra-Vehicular%20Activity%20%28EVA%29%20systems%20during%20the%20six%20Apollo%20missions%20that%20landed%20on%20the%20lunar%20surface%2C%20it%20was%20found%20that%20these%20effects%20can%20take%20many%20forms%20such%20as%20external%20vision%20obscuration%2C%20false%20instrument%20readings%2C%20dust%20coating%20and%20contamination%2C%20loss%20of%20traction%2C%20clogging%20of%20mechanisms%2C%20abrasion%2C%20thermal%20control%20problems%20and%20seal%20failures.%20One%20of%20the%20most%20serious%20effects%20is%20the%20compromising%20of%20astronaut%20health%20by%20irritation%20and%20inhalation%20of%20lunar%20dust.%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3BTherefore%2C%20it%20is%20of%20utmost%20importance%20to%20characterise%20the%20properties%20of%20the%20dust%20particles%20present%20on%20the%20exploration%20sites%20and%20their%20transportation%20mechanisms%20to%20enable%20efficient%20mitigation%20techniques%20to%20be%20put%20in%20place.%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3BThe%20overall%20objective%20of%20the%20DUSTER%20project%20is%20to%20develop%20instrumentation%20and%20technologies%20to%20study%20dust%20particles%20and%20electrostatic%20transportation%20for%20planetary%20and%20small%20body%20exploration%20missions.%20Specifically%2C%20the%20aim%20is%20to%20design%2C%20manufacture%20and%20test%20in%20a%20relevant%20environment%20a%20compact%20multi-sensor%20instrument%20for%20in%20situ%20analysis%20of%20dust%20properties%20%28mechanical%20and%20electrical%29%20and%20electrostatic%20transportation%20that%20can%20be%20used%20on%20a%20small%20lunar%20lander.%20To%20that%20end%2C%20the%20instrument%20includes%3A%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3B-%20A%20dust%20collector%3A%20electrodes%20biased%20at%20high%20potential%20to%20attract%5C%2Fcollect%20dust%20particles%2C%20coupled%20to%20an%20electrometer%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3B-%20Langmuir%20probes%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3B-%20E-field%20probes%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3BUsing%20this%20instrument%2C%20the%20following%20parameters%20will%20be%20derived%3A%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3B-%20Charging%20level%20of%20dust%20as%20a%20function%20of%20the%20environmental%20parameters%20%28illumination%2C%20plasma%20density%20and%20temperature%29%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3B-%20%28gravity%20%2B%20cohesive%20forces%29%5C%2Fcharge%20ratio%20distribution%20of%20dust%20layer%26lt%3B%5C%2Fp%26gt%3B%26lt%3Bp%26gt%3BThese%20two%20parameters%20will%20allow%20the%20determination%20of%20the%20electric%20field%20needed%20to%20attract%5C%2Fcollect%20dust%20according%20to%20the%20environmental%20conditions%20%28illumination%2C%20plasma%20density%20and%20temperature%29%2C%20which%2C%20among%20other%20applications%2C%20will%20allow%20designing%20electrostatic%20dust%20mitigation%20devices%20and%20dust%20sample%20collectors.%26lt%3B%5C%2Fp%26gt%3B%22%2C%22reportNumber%22%3A%22%22%2C%22reportType%22%3A%22other%22%2C%22institution%22%3A%22oral%22%2C%22date%22%3A%222020-03-23%22%2C%22language%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fmeetingorganizer.copernicus.org%5C%2FEGU2020%5C%2FEGU2020-21638.html%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T14%3A52%3A13Z%22%7D%7D%2C%7B%22key%22%3A%22TC5ZS23V%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Balcerak%22%2C%22parsedDate%22%3A%222014-01-07%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EBalcerak%2C%20E.%20Data%20from%20Apollo%20missions%20show%20how%20lunar%20dust%20degrades%20instruments.%20%3Ci%3EEoS%20Transactions%3C%5C%2Fi%3E%20%3Cb%3E95%3C%5C%2Fb%3E%2C%2012%26%23×2013%3B12%20%282014%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Data%20from%20Apollo%20missions%20show%20how%20lunar%20dust%20degrades%20instruments%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ernie%22%2C%22lastName%22%3A%22Balcerak%22%7D%5D%2C%22abstractNote%22%3A%22Apollo%20astronauts%20encountered%20very%20fine%2C%20powdery%2C%20abrasive%20lunar%20dust%2C%20which%20stuck%20to%20scientific%20instruments%20and%20caused%20damage%20and%20sometimes%20overheating%20and%20failure.%20To%20measure%20the%20effects%20of%20lunar%20dust%2C%20each%20of%20the%20first%20four%20Apollo%20expeditions%20left%20a%20set%20of%20solar%20cells%20on%20the%20Moon%2C%20and%20data%20were%20transmitted%20to%20Earth%20from%201969%20to%201976.%22%2C%22date%22%3A%222014-01-07%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1002%5C%2F2014EO010025%22%2C%22ISSN%22%3A%220096-3941%2C%202324-9250%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fagupubs.onlinelibrary.wiley.com%5C%2Fdoi%5C%2F10.1002%5C%2F2014EO010025%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T14%3A47%3A20Z%22%7D%7D%2C%7B%22key%22%3A%22KV8MVTQL%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Cain%22%2C%22parsedDate%22%3A%222010%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ECain%2C%20J.%20R.%20Lunar%20dust%3A%20The%20Hazard%20and%20Astronaut%20Exposure%20Risks.%20%3Ci%3EEarth%20Moon%20Planets%3C%5C%2Fi%3E%20%3Cb%3E107%3C%5C%2Fb%3E%2C%20107%26%23×2013%3B125%20%282010%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Lunar%20dust%3A%20The%20Hazard%20and%20Astronaut%20Exposure%20Risks%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Cain%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%2212%5C%2F2010%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs11038-010-9365-0%22%2C%22ISSN%22%3A%220167-9295%2C%201573-0794%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs11038-010-9365-0%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T14%3A30%3A03Z%22%7D%7D%2C%7B%22key%22%3A%223TPZFEIM%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Currie%20and%20Prochazka%22%2C%22parsedDate%22%3A%222015%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3ECurrie%2C%20D.%20%26amp%3B%20Prochazka%2C%20I.%20Lunar%20laser%20ranging%20and%20limits%20due%20to%20the%20Earth%26%23×2019%3Bs%20atmosphere.%20in%20%3Ci%3ELaser%20Communication%20and%20Propagation%20through%20the%20Atmosphere%20and%20Oceans%20IV%3C%5C%2Fi%3E%20vol.%209614%2081%26%23×2013%3B88%20%28SPIE%2C%202015%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22conferencePaper%22%2C%22title%22%3A%22Lunar%20laser%20ranging%20and%20limits%20due%20to%20the%20Earth%5Cu2019s%20atmosphere%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Douglas%22%2C%22lastName%22%3A%22Currie%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ivan%22%2C%22lastName%22%3A%22Prochazka%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222015%22%2C%22proceedingsTitle%22%3A%22Laser%20Communication%20and%20Propagation%20through%20the%20Atmosphere%20and%20Oceans%20IV%22%2C%22conferenceName%22%3A%22%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.spiedigitallibrary.org%5C%2Fconference-proceedings-of-spie%5C%2F9614%5C%2F96140C%5C%2FLunar-laser-ranging-and-limits-due-to-the-Earths-atmosphere%5C%2F10.1117%5C%2F12.2190834.short%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T14%3A00%3A21Z%22%7D%7D%2C%7B%22key%22%3A%22DGHWC88Z%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Purves%22%2C%22parsedDate%22%3A%221974%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EPurves%2C%20C.%20G.%20%3Ci%3EGeophysical%20Aspects%20of%20Atmospheric%20Refraction%3C%5C%2Fi%3E.%20%28Naval%20Research%20Laboratory%2C%201974%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22Geophysical%20aspects%20of%20atmospheric%20refraction%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Charles%20G.%22%2C%22lastName%22%3A%22Purves%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221974%22%2C%22language%22%3A%22%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Ff5len.free.fr%5C%2FPDF%5C%2FrGeophysical%2520Aspects%2520of%2520Atmospheric%2520Refraction.pdf%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T13%3A56%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22LMQVX32U%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EAtmospheric%20effects%20impact%20the%20performance%20of%20laser…%20-%20Google%20Scholar.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fscholar.google.com%5C%2Fscholar%3Fhl%3Den%26as_sdt%3D0%252C5%26q%3DAtmospheric%2Beffects%2Bimpact%2Bthe%2Bperformance%2Bof%2Blaser%2Bradar%2Bsystems%252C%2Bincluding%2Bmolecular%2Band%2Baerosol%2Bextinction%2Band%2Boptical%2Bturbulence%252C%2Bfor%2Bwavelengths%2Bbeyond%2B1.4%2Bmicrons.%2B%255BD.%2BH.%2BLeslie%252C%2BD.%2BYoumans%252C%2B1995%255D%26btnG%3D%27%3Ehttps%3A%5C%2F%5C%2Fscholar.google.com%5C%2Fscholar%3Fhl%3Den%26as_sdt%3D0%252C5%26q%3DAtmospheric%2Beffects%2Bimpact%2Bthe%2Bperformance%2Bof%2Blaser%2Bradar%2Bsystems%252C%2Bincluding%2Bmolecular%2Band%2Baerosol%2Bextinction%2Band%2Boptical%2Bturbulence%252C%2Bfor%2Bwavelengths%2Bbeyond%2B1.4%2Bmicrons.%2B%255BD.%2BH.%2BLeslie%252C%2BD.%2BYoumans%252C%2B1995%255D%26btnG%3D%3C%5C%2Fa%3E.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22webpage%22%2C%22title%22%3A%22Atmospheric%20effects%20impact%20the%20performance%20of%20laser…%20-%20Google%20Scholar%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fscholar.google.com%5C%2Fscholar%3Fhl%3Den%26as_sdt%3D0%252C5%26q%3DAtmospheric%2Beffects%2Bimpact%2Bthe%2Bperformance%2Bof%2Blaser%2Bradar%2Bsystems%252C%2Bincluding%2Bmolecular%2Band%2Baerosol%2Bextinction%2Band%2Boptical%2Bturbulence%252C%2Bfor%2Bwavelengths%2Bbeyond%2B1.4%2Bmicrons.%2B%255BD.%2BH.%2BLeslie%252C%2BD.%2BYoumans%252C%2B1995%255D%26btnG%3D%22%2C%22language%22%3A%22%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T13%3A54%3A04Z%22%7D%7D%2C%7B%22key%22%3A%22A87AQEIR%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Zhang%20et%20al.%22%2C%22parsedDate%22%3A%222014%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EZhang%2C%20N.%2C%20Wu%2C%20S.%20%26amp%3B%20Shen%2C%20C.%20Analysis%20of%20Effect%20of%20%26%23x3B3%3B%20Radiation%20Angle%20on%20the%20Photons%20Altimeter.%20%3Ci%3EAerospace%20Return%20and%20Remote%20Sensing%3C%5C%2Fi%3E%20%3Cb%3E35%3C%5C%2Fb%3E%2C%2037%26%23×2013%3B41%20%282014%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Analysis%20of%20Effect%20of%20%5Cu03b3%20Radiation%20Angle%20on%20the%20Photons%20Altimeter%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Nan%22%2C%22lastName%22%3A%22Zhang%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Shitong%22%2C%22lastName%22%3A%22Wu%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Chao%22%2C%22lastName%22%3A%22Shen%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222014%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T13%3A41%3A45Z%22%7D%7D%2C%7B%22key%22%3A%22PG5Z8PV7%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Gebhardt%22%2C%22parsedDate%22%3A%221976-06-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EGebhardt%2C%20F.%20G.%20High%20power%20laser%20propagation.%20%3Ci%3EAppl.%20Opt.%3C%5C%2Fi%3E%20%3Cb%3E15%3C%5C%2Fb%3E%2C%201479%20%281976%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22High%20power%20laser%20propagation%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Frederick%20G.%22%2C%22lastName%22%3A%22Gebhardt%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221976-06-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1364%5C%2FAO.15.001479%22%2C%22ISSN%22%3A%220003-6935%2C%201539-4522%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fopg.optica.org%5C%2Fabstract.cfm%3FURI%3Dao-15-6-1479%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T13%3A32%3A40Z%22%7D%7D%2C%7B%22key%22%3A%22IPA7ERT2%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Gebhardt%22%2C%22parsedDate%22%3A%221976%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EGebhardt%2C%20F.%20High%20power%20laser%20propagation.%20%3Ci%3EApplied%20optics%3C%5C%2Fi%3E%20%3Cb%3E15%206%3C%5C%2Fb%3E%2C%201479%26%23×2013%3B93%20%281976%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22High%20power%20laser%20propagation.%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22F.%22%2C%22lastName%22%3A%22Gebhardt%22%7D%5D%2C%22abstractNote%22%3A%22High%20power%20laser%20beams%20propagating%20in%20the%20atmosphere%20are%20subjected%20to%20a%20variety%20of%20effects%2C%20the%20most%20important%20of%20which%20are%20absorption%2C%20scattering%2C%20turbulence%20induced%20beam%20spreading%20and%20wander%2C%20thermal%20blooming%2C%20and%20gas%20breakdown.%20In%20this%20paper%20simplified%20models%20are%20used%20to%20show%20how%20the%20various%20atmospheric%20effects%20interrelate%20and%20impact%20on%20the%20best%20laser%20choice%20for%20high%20power%20applications%20through%20their%20dependence%20on%20the%20laser%20wavelength%20and%20temporal%20mode%20%28e.g.%2C%20cw%20or%20pulsed%29%20of%20operation.%20Results%20for%20sea%20level%20propagation%20at%20seven%20common%20laser%20wavelengths%20varying%20from%200.34%20microm%20to%2010.6%20microm.%20are%20presented%20that%20show%20the%20mid-ir%20wavelengths%20to%20be%20favored%20for%20typical%20turbulence%20and%20aerosol%20scattering%20conditions.%20At%20the%20longer%2010.6-microm%20CO%282%29%20laser%20wavelength%20thermal%20blooming%20is%20dominant%20due%20to%20stronger%20molecular%20absorption%2C%20while%20at%20the%20shorter%20wavelengths%20turbulence%20induced%20beam%20spreading%20and%20aerosol%20absorption%20and%20scattering%20effects%20become%20important%20and%20tend%20to%20limit%20the%20increase%20in%20irradiance%20expected%20on%20the%20basis%20of%20diffraction%20effects%20alone.%22%2C%22date%22%3A%221976%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1364%5C%2FAO.15.001479%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fconsensus.app%5C%2Fpapers%5C%2Fpower-laser-propagation-gebhardt%5C%2F92b11aa670f0519f88ae8e9bab51f362%5C%2F%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T13%3A31%3A23Z%22%7D%7D%2C%7B%22key%22%3A%227FK2REVH%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Bosch%22%2C%22parsedDate%22%3A%222001-01-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EBosch%2C%20T.%20Laser%20ranging%3A%20a%20critical%20review%20of%20usual%20techniques%20for%20distance%20measurement.%20%3Ci%3EOpt.%20Eng%3C%5C%2Fi%3E%20%3Cb%3E40%3C%5C%2Fb%3E%2C%2010%20%282001%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Laser%20ranging%3A%20a%20critical%20review%20of%20usual%20techniques%20for%20distance%20measurement%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thierry%22%2C%22lastName%22%3A%22Bosch%22%7D%5D%2C%22abstractNote%22%3A%22We%20review%20some%20usual%20laser%20range%20%5Cufb01nding%20techniques%20for%20industrial%20applications.%20After%20outlining%20the%20basic%20principles%20of%20triangulation%20and%20time%20of%20%5Cufb02ight%20%5Bpulsed%2C%20phase-shift%20and%20frequency%20modulated%20continuous%20wave%20%28FMCW%29%5D%2C%20we%20discuss%20their%20respective%20fundamental%20limitations.%20Selected%20examples%20of%20traditional%20and%20new%20applications%20are%20also%20brie%5Cufb02y%20presented.%20%5Cu00a9%202001%20Society%20of%20Photo-Optical%20Instrumentation%20Engineers.%22%2C%22date%22%3A%222001-01-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1117%5C%2F1.1330700%22%2C%22ISSN%22%3A%220091-3286%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fopticalengineering.spiedigitallibrary.org%5C%2Farticle.aspx%3Fdoi%3D10.1117%5C%2F1.1330700%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T13%3A21%3A16Z%22%7D%7D%2C%7B%22key%22%3A%22KRSSYPYM%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Weil%22%2C%22parsedDate%22%3A%221973%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EWeil%2C%20T.%20Atmospheric%20Lens%20Effect%3B%20Another%20Loss%20for%20the%20Radar%20Range%20Equation.%20%3Ci%3EIEEE%20Trans.%20Aerosp.%20Electron.%20Syst.%3C%5C%2Fi%3E%20%3Cb%3EAES-9%3C%5C%2Fb%3E%2C%2051%26%23×2013%3B54%20%281973%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Atmospheric%20Lens%20Effect%3B%20Another%20Loss%20for%20the%20Radar%20Range%20Equation%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Weil%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%2201%5C%2F1973%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1109%5C%2FTAES.1973.309700%22%2C%22ISSN%22%3A%220018-9251%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fieeexplore.ieee.org%5C%2Fdocument%5C%2F4103080%5C%2F%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T13%3A17%3A11Z%22%7D%7D%2C%7B%22key%22%3A%22L8BXMYPM%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Weil%22%2C%22parsedDate%22%3A%221973%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EWeil%2C%20T.%20Atmospheric%20Lens%20Effect%3B%20Another%20Loss%20for%20the%20Radar%20Range%20Equation.%20%3Ci%3EIEEE%20Trans.%20Aerosp.%20Electron.%20Syst.%3C%5C%2Fi%3E%20%3Cb%3EAES-9%3C%5C%2Fb%3E%2C%2051%26%23×2013%3B54%20%281973%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Atmospheric%20Lens%20Effect%3B%20Another%20Loss%20for%20the%20Radar%20Range%20Equation%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Weil%22%7D%5D%2C%22abstractNote%22%3A%22A%20small%20additional%20loss%20for%20radar%20range%20calculations%20at%20low%20grazing%20angles%20is%20described.%20This%20loss%20results%20because%20the%20variation%20in%20atmospheric%20refraction%20versus%20altitude%20makes%20the%20atmosphere%20act%20like%20a%20lens%2C%20causing%20thinning%20of%20radar%20signal%20energy%20to%20and%20from%20the%20target%2C%20independent%20of%20frequency.%20The%20magnitude%20of%20loss%20is%20derived%20and%20is%20plotted%20versus%20grazing%20angle%20and%20range.%20The%20maximum%20two-way%20loss%2C%20occurring%20at%20zero%20degrees%20grazing%20angle%20and%20a%20range%20well%20beyond%20the%20atmosphere%2C%20is%202.9%20dB.%22%2C%22date%22%3A%2201%5C%2F1973%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1109%5C%2FTAES.1973.309700%22%2C%22ISSN%22%3A%220018-9251%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fieeexplore.ieee.org%5C%2Fdocument%5C%2F4103080%5C%2F%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T13%3A16%3A56Z%22%7D%7D%2C%7B%22key%22%3A%22ETU6YQZZ%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Pierrottet%20et%20al.%22%2C%22parsedDate%22%3A%222008%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EPierrottet%2C%20D.%20%3Ci%3Eet%20al.%3C%5C%2Fi%3E%20Linear%20FMCW%20Laser%20Radar%20for%20Precision%20Range%20and%20Vector%20Velocity%20Measurements.%20%3Ci%3EMRS%20Proc.%3C%5C%2Fi%3E%20%3Cb%3E1076%3C%5C%2Fb%3E%2C%201076-K04-06%20%282008%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Linear%20FMCW%20Laser%20Radar%20for%20Precision%20Range%20and%20Vector%20Velocity%20Measurements%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Diego%22%2C%22lastName%22%3A%22Pierrottet%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Farzin%22%2C%22lastName%22%3A%22Amzajerdian%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Larry%22%2C%22lastName%22%3A%22Petway%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Bruce%22%2C%22lastName%22%3A%22Barnes%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22George%22%2C%22lastName%22%3A%22Lockard%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Manuel%22%2C%22lastName%22%3A%22Rubio%22%7D%5D%2C%22abstractNote%22%3A%22An%20all%20fiber%20linear%20frequency%20modulated%20continuous%20wave%20%28FMCW%29%20coherent%20laser%20radar%20system%20is%20under%20development%20with%20a%20goal%20to%20aide%20NASA%5Cu2019s%20new%20Space%20Exploration%20initiative%20for%20manned%20and%20robotic%20missions%20to%20the%20Moon%20and%20Mars.%20By%20employing%20a%20combination%20of%20optical%20heterodyne%20and%20linear%20frequency%20modulation%20techniques%20%5B1-3%5D%20and%20utilizing%20state-of-the-art%20fiber%20optic%20technologies%2C%20highly%20efficient%2C%20compact%20and%20reliable%20laser%20radar%20suitable%20for%20operation%20in%20a%20space%20environment%20is%20being%20developed.%20Linear%20FMCW%20lidar%20has%20the%20capability%20of%20high-resolution%20range%20measurements%2C%20and%20when%20configured%20into%20a%20multi-channel%20receiver%20system%20it%20has%20the%20capability%20of%20obtaining%20high%20precision%20horizontal%20and%20vertical%20velocity%20measurements.%20Precision%20range%20and%20vector%20velocity%20data%20are%20beneficial%20to%20navigating%20planetary%20landing%20pods%20to%20the%20preselected%20site%20and%20achieving%20autonomous%2C%20safe%20soft-landing.%20The%20all-fiber%20coherent%20laser%20radar%20has%20several%20important%20advantages%20over%20more%20conventional%20pulsed%20laser%20altimeters%20or%20range%20finders.%20One%20of%20the%20advantages%20of%20the%20coherent%20laser%20radar%20is%20its%20ability%20to%20measure%20directly%20the%20platform%20velocity%20by%20extracting%20the%20Doppler%20shift%20generated%20from%20the%20motion%2C%20as%20opposed%20to%20time%20of%20flight%20range%20finders%20where%20terrain%20features%20such%20as%20hills%2C%20cliffs%2C%20or%20slopes%20add%20error%20to%20the%20velocity%20measurement.%20Doppler%20measurements%20are%20about%20two%20orders%20of%20magnitude%20more%20accurate%20than%20the%20velocity%20estimates%20obtained%20by%20pulsed%20laser%20altimeters%20%5B4%5D.%20In%20addition%2C%20most%20of%20the%20components%20of%20the%20device%20are%20efficient%20and%20reliable%20commercial%20off-the-shelf%20fiber%20optic%20telecommunication%20components.%20This%20paper%20discusses%20the%20design%20and%20performance%20of%20a%20second-generation%20brassboard%20system%20under%20development%20at%20NASA%20Langley%20Research%20Center%20as%20part%20of%20the%20Autonomous%20Landing%20and%20Hazard%20Avoidance%20%28ALHAT%29%20project.%22%2C%22date%22%3A%222008%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1557%5C%2FPROC-1076-K04-06%22%2C%22ISSN%22%3A%220272-9172%2C%201946-4274%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1557%5C%2FPROC-1076-K04-06%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T13%3A15%3A25Z%22%7D%7D%2C%7B%22key%22%3A%22A57CJKTR%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Vaughn%20et%20al.%22%2C%22parsedDate%22%3A%222007%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EVaughn%2C%20J.%20A.%20St.%20%3Ci%3Eet%20al.%3C%5C%2Fi%3E%20Design%20of%20a%20Retro%20Rocket%20Earth%20Landing%20System%20for%20the%20Orion%20Spacecraft.%20in%20%3Ci%3E2007%20IEEE%20Aerospace%20Conference%3C%5C%2Fi%3E%201%26%23×2013%3B12%20%28IEEE%2C%20Big%20Sky%2C%20MT%2C%20USA%2C%202007%29.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27http%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1109%5C%2FAERO.2007.352819%27%3Ehttp%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1109%5C%2FAERO.2007.352819%3C%5C%2Fa%3E.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22conferencePaper%22%2C%22title%22%3A%22Design%20of%20a%20Retro%20Rocket%20Earth%20Landing%20System%20for%20the%20Orion%20Spacecraft%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joshua%20A.%20St.%22%2C%22lastName%22%3A%22Vaughn%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Gurkirpal%22%2C%22lastName%22%3A%22Singh%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ravi%22%2C%22lastName%22%3A%22Prakash%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robert%20H.%22%2C%22lastName%22%3A%22Frisbee%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22James%20M.%22%2C%22lastName%22%3A%22Corliss%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robin%20D.%22%2C%22lastName%22%3A%22Tutterow%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222007%22%2C%22proceedingsTitle%22%3A%222007%20IEEE%20Aerospace%20Conference%22%2C%22conferenceName%22%3A%222007%20IEEE%20Aerospace%20Conference%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1109%5C%2FAERO.2007.352819%22%2C%22ISBN%22%3A%22978-1-4244-0524-4%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fieeexplore.ieee.org%5C%2Fdocument%5C%2F4161335%5C%2F%22%2C%22collections%22%3A%5B%225NZA4E68%22%5D%2C%22dateModified%22%3A%222023-12-23T13%3A13%3A25Z%22%7D%7D%2C%7B%22key%22%3A%2224CKEYLU%22%2C%22library%22%3A%7B%22id%22%3A13285244%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Vaughn%20et%20al.%22%2C%22parsedDate%22%3A%222007%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%20style%3D%5C%22clear%3A%20left%3B%20%5C%22%3E%5Cn%20%20%20%20%3Cdiv%20class%3D%5C%22csl-left-margin%5C%22%20style%3D%5C%22float%3A%20left%3B%20padding-right%3A%200.5em%3B%20text-align%3A%20right%3B%20width%3A%201em%3B%5C%22%3E1.%3C%5C%2Fdiv%3E%3Cdiv%20class%3D%5C%22csl-right-inline%5C%22%20style%3D%5C%22margin%3A%200%20.4em%200%201.5em%3B%5C%22%3EVaughn%2C%20J.%20A.%20S.%20%3Ci%3Eet%20al.%3C%5C%2Fi%3E%20Design%20of%20a%20retro%20rocket%20earth%20landing%20system%20for%20the%20Orion%20spacecraft.%20in%20%3Ci%3E2007%20IEEE%20Aerospace%20Conference%3C%5C%2Fi%3E%201%26%23×2013%3B12%20%28IEEE%2C%202007%29.%3C%5C%2Fdiv%3E%5Cn%20%20%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22conferencePaper%22%2C%22title%22%3A%22Design%20of%20a%20retro%20rocket%20earth%20landing%20system%20for%20the%20Orion%20spacecraft%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joshua%20A%20St%22%2C%22lastName%22%3A%22Vaughn%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Gurkirpal%22%2C%22lastName%22%3A%22Singh%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ravi%22%2C%22lastName%22%3A%22Prakash%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robert%20H%22%2C%22lastName%22%3A%22Frisbee%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22James%20M%22%2C%22lastName%22%3A%22Corliss%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robin%20D%22%2C%22lastName%22%3A%22Tutterow%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222007%22%2C%22proceedingsTitle%22%3A%222007%20IEEE%20Aerospace%20Conference%22%2C%22conferenceName%22%3A%22%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-12-23T13%3A11%3A58Z%22%7D%7D%5D%7D
1.
Ye, W., Wu, H., Tan, Z. & Zou, Q. An Adaptive Time Stepping Algorithm and Its Application to Platelet Aggregation Simulation. in
2021 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom) 1360–1369 (IEEE, New York City, NY, USA, 2021).
http://doi.org/10.1109/ISPA-BDCloud-SocialCom-SustainCom52081.2021.00186 .
1.
Shi, Y. et al. Study of adaptive symplectic methods for simulating charged particle dynamics. Journal of Computational Dynamics 6 , 429–448 (2019).
1.
Qiao, Z., Zhang, Z. & Tang, T. An Adaptive Time-Stepping Strategy for the Molecular Beam Epitaxy Models. SIAM J. Sci. Comput. 33 , 1395–1414 (2011).
1.
all the zeros of 𝜀(k�, 𝜔�) lie in the lower half 𝜔 plane.
1.
𝛿̃ NS 𝛽 (k, v, 𝜔)= 1 (2𝜋)3 d3r ∞ 0 dt 𝛿N𝛽 (r − vt, v,0)e−i(k⋅r−𝜔t).
1.
∇2𝛿𝜙 =−1 𝜀0 𝛽 q𝛽 d3v 𝛿N𝛽(r − vt, v,0) + q𝛽 m𝛽 t 0 dt� ∇𝛿𝜙(r − v(t − t�), t�) ⋅ 𝜕f𝛽 (v) 𝜕v .
1.
r𝛼 (t)=r(0) 𝛼 (t)− q𝛼 m𝛼 t 0 (t − t�)∇𝛿𝜙(r𝛼(t�), t�) dt�.
1.
and the contributions from the other parts of the contour including the horizontal lines and circles around the poles 𝜔 k encountered decaying exponentially with t can be discarded.
1.
the pole at 𝜔� = k� ⋅ v𝛼 and the poles 𝜔� k (k = 1, 2, ⋯) corresponding to the zeros of 𝜀(k�, 𝜔�).
1.
Fried, B. D. & Conte, S. D. The Plasma Dispersion Function.
1.
Percival, D. J. & Robinson, P. A. Generalized plasma dispersion functions. Journal of Mathematical Physics 39 , 3678–3693 (1998).
1.
Summers, D. & Thorne, R. M. The modified plasma dispersion function. Physics of Fluids B: Plasma Physics 3 , 1835–1847 (1991).
1.
Rutherford, Lord. The Origin of the Gamma-Rays. The Scientific Monthly 34 , 483–486 (1932).
1.
Wolfendale, A. A brief review of gamma ray astronomy. Nuclear Physics B-Proceedings Supplements 22 , 80–85 (1991).
1.
Wolfendale, A. A BRIEF REVIEW OF GAMMA RAY ASTRONOWi.
1.
Saxton, J. A. The influence of atmospheric conditions on radar performance. The Journal of Navigation 11 , 290–303 (1958).
1.
Fahey, T., Islam, M., Gardi, A. & Sabatini, R. Laser beam atmospheric propagation modelling for aerospace LIDAR applications. Atmosphere 12 , 918 (2021).
1.
Der, S., Redman, B. & Chellappa, R. Simulation of error in optical radar range measurements. Applied Optics 36 , 6869–6874 (1997).
1.
Wu, J., Wang, C. & Song, S. 月球着陆器典型故障模式分析(Analysis of Typical Fault Modes of Lunar Landers). Journal of Astronautics 35 , 633–638 (2014).
1.
Wang, H. & Richardson, M. I. The origin, evolution, and trajectory of large dust storms on Mars during Mars years 24–30 (1999–2011). Icarus 251 , 112–127 (2015).
1.
孙占海 & 罗克. “神舟八号” 飞船 γ 源高度控制装置安装工具和方法的改进. 航天器环境工程 28 , 650–651 (2011).
1.
van Eijk, A. M. & Stein, K. Atmospheric and laser propagation. Technologies for Optical Countermeasures XIV 10435 , 42–51 (2017).
1.
张楠, 吴世通 & 沈超. γ源辐射角度对光子高度计性能的影响分析(Analysis of Effect of γ Radiation Angle on the Photons Altimeter). 航天返回与遥感 35 , 37–41 (2014).
1.
McLeod, R. R., Villalobos, I. P., Tomita, Y. & Sheridan, J. T. Photosensitive Materials and their Applications. in Proc. of SPIE Vol vol. 11367 1136701–1 (2020).
1.
Leslie, D. H. & Youmans, D. G. Atmospheric effects on eye-safe airborne laser radar. in Beam Control, Diagnostics, Standards, and Propagation vol. 2375 17–29 (SPIE, 1995).
1.
Dumont, R. Waves in Plasmas . (2007).
1.
Bobylev, A. V. & Nanbu, K. Theory of collision algorithms for gases and plasmas based on the Boltzmann equation and the Landau-Fokker-Planck equation. Phys. Rev. E 61 , 4576–4586 (2000).
1.
Coulomb collisions in plasma can be treated as successive binary collisions @5#.
1.
Cohen, R. S., Spitzer, L. & Routly, P. McR. The Electrical Conductivity of an Ionized Gas. Phys. Rev. 80 , 230–238 (1950).
1.
Doner, A., Horányi, M., Faller, J., Fontanese, J. & Munsat, T. Restoring light transmission of dusty glass surfaces on the Moon. Advances in Space Research 68 , 4050–4055 (2021).
1.
Zhao, J., Du, X., Song, Y., Zhu, C. & Chen, P. Study on the influence of aerosol macroscopic characteristics on backscattering signals. in
Third International Conference on Photonics and Optical Engineering (ed. Tian, A.) 103 (SPIE, Xi’an, China, 2019).
http://doi.org/10.1117/12.2522031 .
1.
Stein, K., Gladysz, S., Seiffer, D. & Zepp, A. Atmospheric limitations on the performance of electro-optical systems: a brief overview. in (eds. Van Eijk, A. M. J., Davis, C. C. & Hammel, S. M.) 92240U (San Diego, California, United States, 2014).
http://doi.org/10.1117/12.2064631 .
1.
Cain, J. R. Lunar dust: The Hazard and Astronaut Exposure Risks. Earth Moon Planets 107 , 107–125 (2010).
1.
Balcerak, E. Data from Apollo missions show how lunar dust degrades instruments. EoS Transactions 95 , 12–12 (2014).
1.
Cain, J. R. Lunar dust: The Hazard and Astronaut Exposure Risks. Earth Moon Planets 107 , 107–125 (2010).
1.
Currie, D. & Prochazka, I. Lunar laser ranging and limits due to the Earth’s atmosphere. in Laser Communication and Propagation through the Atmosphere and Oceans IV vol. 9614 81–88 (SPIE, 2015).
1.
Purves, C. G. Geophysical Aspects of Atmospheric Refraction . (Naval Research Laboratory, 1974).
1.
Zhang, N., Wu, S. & Shen, C. Analysis of Effect of γ Radiation Angle on the Photons Altimeter. Aerospace Return and Remote Sensing 35 , 37–41 (2014).
1.
Gebhardt, F. G. High power laser propagation. Appl. Opt. 15 , 1479 (1976).
1.
Gebhardt, F. High power laser propagation. Applied optics 15 6 , 1479–93 (1976).
1.
Bosch, T. Laser ranging: a critical review of usual techniques for distance measurement. Opt. Eng 40 , 10 (2001).
1.
Weil, T. Atmospheric Lens Effect; Another Loss for the Radar Range Equation. IEEE Trans. Aerosp. Electron. Syst. AES-9 , 51–54 (1973).
1.
Pierrottet, D. et al. Linear FMCW Laser Radar for Precision Range and Vector Velocity Measurements. MRS Proc. 1076 , 1076-K04-06 (2008).
1.
Vaughn, J. A. St.
et al. Design of a Retro Rocket Earth Landing System for the Orion Spacecraft. in
2007 IEEE Aerospace Conference 1–12 (IEEE, Big Sky, MT, USA, 2007).
http://doi.org/10.1109/AERO.2007.352819 .
1.
Vaughn, J. A. S. et al. Design of a retro rocket earth landing system for the Orion spacecraft. in 2007 IEEE Aerospace Conference 1–12 (IEEE, 2007).
Attachments
γ射线测距 Data 12-9