Question Link: Here
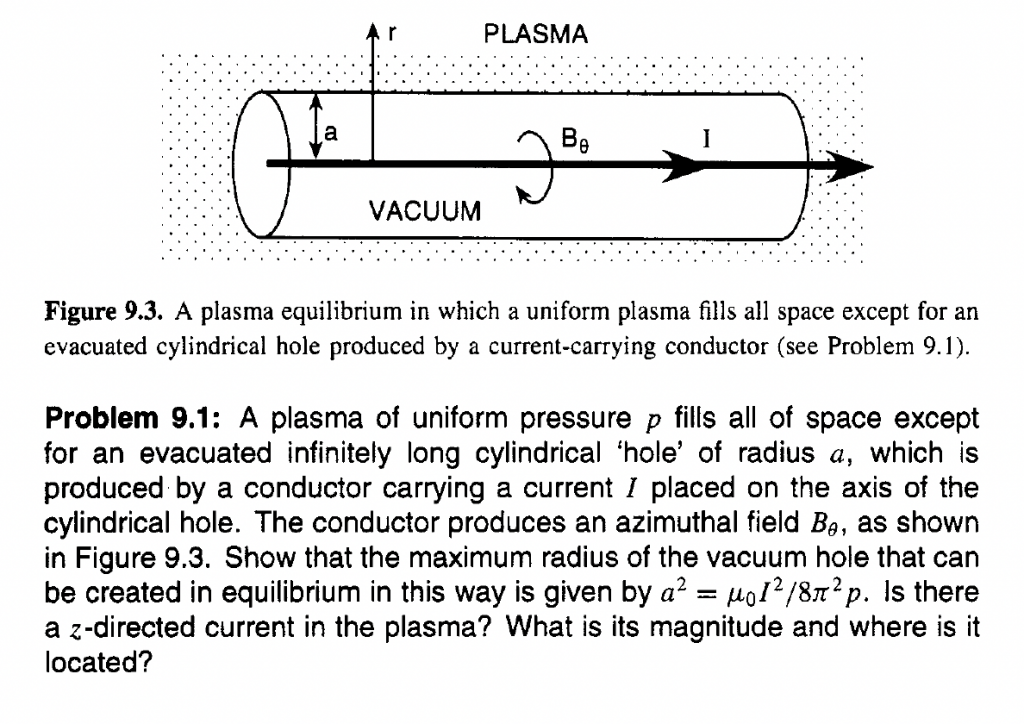
To solve this problem, we need to understand the balance of forces in the plasma and the magnetic field created by the current-carrying conductor. The equilibrium condition requires that the magnetic pressure from the azimuthal field \(B_{\theta}\) balances the plasma pressure \(p\) at the boundary of the evacuated hole. Let’s proceed step by step:
Step 1: Write down the expression for the magnetic pressure. The magnetic pressure can be expressed as \(p_{magnetic} = \frac{B^2}{2\mu_0}\), where \(B\) is the magnetic field strength and \(\mu_0\) is the permeability of free space.
Step 2: Express the magnetic field \(B_{\theta}\) around a current-carrying conductor. According to Ampère’s law, the magnetic field around a long, straight conductor carrying a current \(I\) is given by \(B_{\theta} = \frac{\mu_0 I}{2\pi r}\), where \(r\) is the radial distance from the conductor.
Step 3: Substitute \(B_{\theta}\) into the magnetic pressure formula. Substituting the expression for \(B_{\theta}\) from Step 2 into the magnetic pressure formula from Step 1 gives: \[p_{magnetic} = \frac{(\frac{\mu_0 I}{2\pi r})^2}{2\mu_0} = \frac{\mu_0 I^2}{8\pi^2 r^2}\]
Step 4: Set the magnetic pressure equal to the plasma pressure. For equilibrium, the magnetic pressure at the boundary of the evacuated hole (radius \(a\)) must balance the plasma pressure \(p\). Therefore, we set \(p_{magnetic} = p\) and solve for \(a\): \[p = \frac{\mu_0 I^2}{8\pi^2 a^2}\]
Step 5: Solve for \(a^2\). Rearranging the equation from Step 4 to solve for \(a^2\) gives: \[a^2 = \frac{\mu_0 I^2}{8\pi^2 p}\]
Step 6: Recognize the given condition \(o^2 = \mu_0 I^2\). The problem statement or the book might define \(o^2 = \mu_0 I^2\) as a given condition or notation. Substituting this into the equation from Step 5 yields: \[a^2 = \frac{o^2}{8\pi^2 p}\]
Step 7: Address the question about the z-directed current. The current that creates the azimuthal magnetic field \(B_{\theta}\) is located on the axis of the cylindrical hole and is directed along the \(z\)-axis. This is the current \(I\) carried by the conductor. There is no additional z-directed current in the plasma itself; the plasma’s role is to provide pressure that balances the magnetic pressure at the boundary.
Conclusion: The maximum radius \(a\) of the vacuum hole that can be created in equilibrium by a conductor carrying a current \(I\) is given by \(a^2 = \frac{o^2}{8\pi^2 p}\), where \(o^2 = \mu_0 I^2\). The z-directed current is the current \(I\) in the conductor, and it is located on the axis of the cylindrical hole.
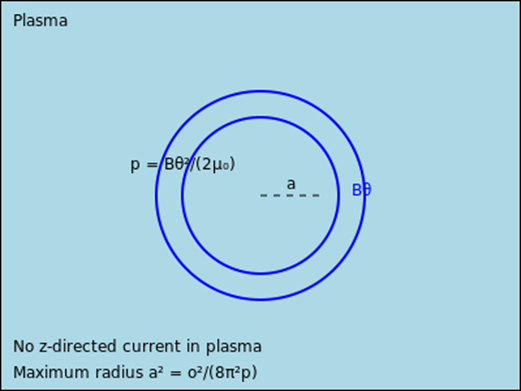
上面的题解有点问题,我自己写一下。
由uniform p可以得到,等离子体区域没有B。因为B会造成\(p_\parallel\neq p_\perp\)。
所以等离子体和真空的交界有抗磁电流\(I_D=-I\).
求\(a^2\)
\[p(r)=\left\{\begin{aligned}0 \quad r<a\\p \quad r>a\\ \end{aligned}\right.\]
根据书中公式9.11有(r=0处理起来有点啰嗦,就用\(\infty\)代替了)
\[
\left\{
\begin{array}{l}
-\frac{B^2 (a – \delta)}{2\mu_0} – \frac{1}{\mu_0} \int_{\infty}^{a-\delta} \frac{B^2(r)}{r} \, dr = 0 \\
-\frac{B^2 (a + \delta)}{2\mu_0} – \frac{1}{\mu_0} \int_{\infty}^{a+\delta} \frac{B^2(r)}{r} \, dr = p
\end{array}
\right.
\]
两式作差,并取极限\(\delta\to 0\)(积分项极限为0),
\[\frac{B^2(a^-)}{2\mu_0}-\frac{B^2(a^+)}{2\mu_0}=p,\quad \text{where}\quad B^2(a^+)=0\]
\[\frac{B^2(a^-)}{2\mu_0}=p\rightarrow (\mu_0 I/2\pi a)^2=2\mu_0 p\]
所以\(a^2=\mu_0 I^2 / 8\pi^2 p\)