The Dielectric Tensor

The dielectric tensor for a hot plasma, which conforms the Maxwellian distribution, in a magnetic field can be expressed as

\[
\mathbf{K}(\text{Stix}) =
\begin{bmatrix}
K_1 & K_2 & K_4 \\
-K_2 & K_1 + K_0 & -K_5 \\
K_4 & K_5 & K_3
\end{bmatrix},
\]

where

\begin{align}
K_0 &= 2 \sum_j \frac{\omega_{pj}^2 e^{-\lambda_j}}{\omega k_{\parallel} v_{\parallel j}} \sum_{n=-\infty}^{\infty} \lambda_j (I_n – I_n’) A_{nj}, \\
K_1 &= 1 + \sum_j \frac{\omega_{pj}^2 e^{-\lambda_j}}{\omega k_{\parallel} v_{\parallel j}} \sum_{n=-\infty}^{\infty} \frac{n^2 I_n}{\lambda_j} A_{nj}, \\
K_2 &= i \sum_j \frac{\omega_{pj}^2 e^{-\lambda_j}}{\omega k_{\parallel} v_{\parallel j}} \sum_{n=-\infty}^{\infty} n (I_n – I_n’) A_{nj}, \\
K_3 &= 1 – \sum_j \frac{\omega_{pj}^2 e^{-\lambda_j}}{\omega k_{\parallel} v_{\parallel j}} \sum_{n=-\infty}^{\infty} I_n \left( \frac{\omega + n \omega_{c j}}{k_{\parallel} V_{\parallel j}} \right) B_{nj}, \\
K_4 &= \sum_j \frac{k_{\parallel} \omega_{pj}^2 e^{-\lambda_j}}{k_{\parallel} \omega c_j} \sum_{n=-\infty}^{\infty} \frac{n I_n}{\lambda_j} C_{nj}, \\
K_5 &= i \sum_j \frac{k_{\perp} \varepsilon_{j} \omega_{pj}^2 e^{-\lambda_j}}{k_{\parallel} \omega c_j} \sum_{n = -\infty}^{\infty} (I_n – I_n’) C_{nj},
\end{align}

and

\begin{align}
A_{nj} &= \left( 1 – \frac{k_{\parallel} V_{0j}}{\omega} \right) Z(\zeta_{nj}) + \frac{k_{\parallel} v_{\parallel j}}{\omega} \left( 1 – \frac{T_{\perp j}}{T_{\parallel j}} \right) \frac{Z'(\zeta_{nj})}{2}, \\
B_{nj} &= \left[ 1 + \frac{n \omega_{c_j}}{\omega} \left(1 – \frac{T_{\parallel j}}{T_{\perp j}}\right) \right] Z'(\zeta_{nj}) + \frac{2n\omega_{c_j}T_{\parallel j}V_{0j}}{\omega T_{\perp j} v_{\parallel j}} \left( Z(\zeta_{nj}) + \frac{k_{\parallel}v_{\parallel j}}{\omega + n \omega_{c_j}} \right), \\
C_{nj} &= \frac{n \omega_{c_j} V_{0j} Z(\zeta_{nj})}{\omega v_{\parallel j}} + \left[ \frac{T_{\perp j}}{T_{\parallel j}} – \frac{n \omega_{c_j}}{\omega} \left( 1 – \frac{T_{\parallel j}}{T_{\perp j}} \right) \right] \frac{Z'(\zeta_{nj})}{2}.
\end{align}

Here \( n \) refers to the harmonic and \( j \) to the species number, \( \omega_{pj} \) is the plasma angular frequency, \( \omega_{cj} \) the cyclotron angular frequency, \( \lambda_j = 0.5 k^2 \rho_{Lj}^2 \) the FLR parameter, \( \rho_{Lj} = v_{\perp j}/\omega_{cj} \) the Larmor radius, \( v_{\perp j} \) the perpendicular thermal velocity, \( v_{\parallel j} \) the parallel thermal velocity, \( v_{0j} \) the net parallel flow velocity, \( I_n = I_n(\lambda_j) \) the modified Bessel function of order \( n \), \( T_{\perp j} \) and \( T_{\parallel j} \) the perpendicular and parallel temperatures, respectively, \( Z(\zeta_{nj}) \) the plasma dispersion function evaluated at \( \zeta_{nj} = (\omega + n\omega_{cj} – k_{\parallel}v_{0j})/(k_{\parallel}v_{\parallel j}) \), \( \varepsilon_j = q_j/|q_j| \) the charge sign and \( q_j \) the charge.

The MATLAB Code

Evaluating K tensor corresponding to certain wave properties

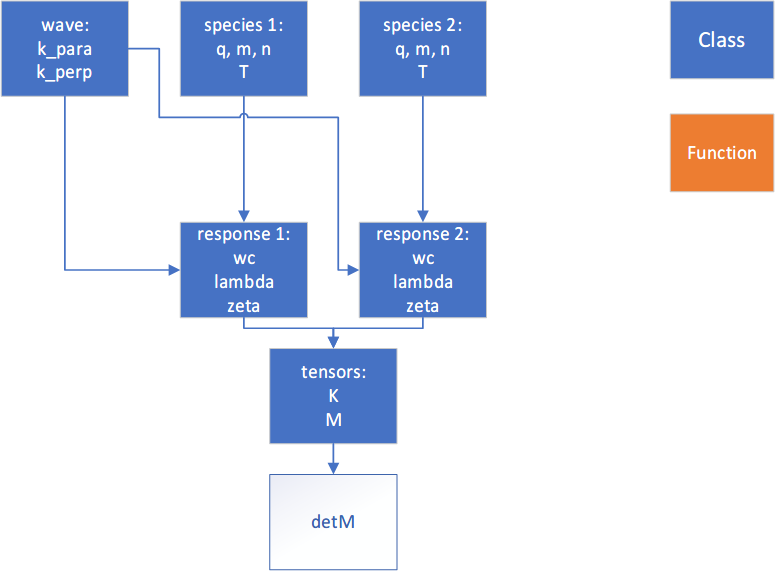
As depicted in Figure [alm label=’flow1′], a ‘species’ object is created for each species within the plasma. Given the wave properties (\(\omega, k_\parallel\), and \(k_\perp\)), we obtain the responses of each species to the wave, including \(\omega_{cj}\) and \(\lambda_{j}\) (refer to ). Finally, the dielectric tensor is evaluated, and the plasma dispersion relation (LHS) is determined by calculating \(\det M\), where:

\begin{equation}
M = \left(
\begin{array}{ccc}
\kappa_{xx} – k_{z}^2 – k_{y}^2 & \kappa_{xy} + k_{x}k_{y} & \kappa_{xz} + k_{x}k_{z} \\
\kappa_{yx} + k_{y}k_{x} & \kappa_{yy} – k_{z}^2 – k_{x}^2 & \kappa_{yz} + k_{y}k_{z} \\
\kappa_{zx} + k_{z}k_{x} & \kappa_{zy} + k_{z}k_{y} & \kappa_{zz} – k_{\perp}^2
\end{array}
\right)
\end{equation}

Here, \(\kappa_j = K_j\). By rotating the coordinates and setting \(k_y=0\), we simplify the expression to \(k_\perp=k_x\).

In cases where waves are emitted from an antenna, \(k_\parallel\) is given, while \(k_\perp\) remains unknown. For any arbitrary \(k_\perp\), typically \(\det M\) does not equal zero. However, by exploring different \(k_\perp\), we can always discover the zeros of \(F(k_\perp)\equiv \det M(k_\perp)\).

FSOLVE: find zeros of \(F(k_\perp)\) by iterative algorithms

In MATLAB, the method is rather simple:

kx = fsolve(@getDetM, kx0);

Results and Discussion

1D Solver

The simplified 1D model configuration for the EAST tokamak is illustrated in Figure [alm label=’1dconfig’]. In terms of species, the plasma comprises hydrogen (H), deuterium (D), and electrons. The number densities of H and D are (0.1 n_e) and (0.9 n_e) respectively. Subsequently, (k_x) (also denoted as (k_{\perp})) is derived by the solver based on the plasma profile at various locations, ranging from 1.6m to 2.35m. Within the plasma, two lower hybrid wave modes are present: the fast wave and the slow wave. Their corresponding (k_x)’s are determined by supplying distinct initial values to the fsolve function (refer to Figure [alm label=’kx’]). The initial values, on the other hand, is from cold plasma solutions.

It is evident that the slow wave is unable to propagate within the plasma except within the edge areas. In contrast, the fast wave demonstrates the capability to propagate across most regions and experiences absorption (or reflection) at the core. This phenomenon aligns with the observation that resonance occurs in the core, as indicated by the cold plasma solution.

2D Solver

Given plasma profiles on a R-Z plain, we can similarly evaluate the 2D dispersion relation. Certain improvements, however, must be made to accelerate the computation and guarantee accuracy:

• Dawson function from Faddeeva package (Algorithm of Steven G. Johnson, Faddeeva Package – AbInitio (mit.edu)), which is significantly faster than the built-in MATLAB function dawson.
• Parallel computing. For efficient computation on 2D grids, the workload is distributed across multiple processors. Utilizing parfor, each processor can calculate one row concurrently, maximizing computational efficiency.
• Update the initial values: Following the initial calculation, it’s observed that \(\det M\) still doesn’t reach zero on certain grids. This discrepancy arises from using a uniform initial value across all grids, which is anticipated to be inaccurate because while the wave propagates in most areas (\(text{Im}(k_x)\approx 0\)), it can be absorbed in other areas (\(\text{Im}(k_x)\gg \text{Re}(k_x)\)). However, for each grid (i, j), we can employ the mean value of its eight neighboring grids as the initial guess. This approach leverages the continuity of plasmas and allows us to run the solver for a second time to obtain calibrated results.

Then, the dielectric tensor can be evaluated from \(k_x\), and will be exported to COMSOL for further analysis of wave properties.

Reference

Downloads