Dielectric Tensor
Linearized equation of motion:
\[ -i\omega m_s \vb{u_{1s}}=q_s (\vb{E_1}+\vb{u_{1s}}\times \vb{B_0})\].
Let \(\hat{z}\) be the direction of \(\vb{B_0}\), and then we have the equation of motion in components:
\begin{equation}
\left\{
\begin{array}{l}
u_{xs} = \frac{iq_{s}}{m_{s}(\omega^2 – \omega_{cs}^2)}(\omega E_{x} + i\omega_{cs} E_{y}) \\
u_{ys} = \frac{iq_{s}}{m_{s}(\omega^2 – \omega_{cs}^2)}(-i\omega_{cs} E_{x} + \omega E_{y}) \\
u_{zs} = \frac{iq_{s}}{m_{s}\omega} E_{z}
\end{array}
\right.
\end{equation}
The diectric (permittivity) tensor is defined as \[\va{\va{K}}=1+\frac{i}{\omega\epsilon_0} \va{\va{\sigma}},\] from which we obtain
\begin{equation}
\va{\va{K}} =
\begin{pmatrix}
S & -iD & 0 \\
iD & S & 0 \\
0 & 0 & P
\end{pmatrix},
\end{equation}
where
\[
\begin{array}{l}
R = 1 – \sum_{s} \frac{\omega_{ps}^2}{\omega(\omega + \Omega_{cs})}, \\
L = 1 – \sum_{s} \frac{\omega_{ps}^2}{\omega(\omega – \Omega_{cs})},\\
P = 1 – \sum_{s} \frac{\omega_{ps}^2}{\omega^2},\\
S = \frac{1}{2}(R + L) = 1 – \sum_{s} \frac{\omega_{ps}^2}{\omega^2 – \Omega_{cs}^2},\\
\end{array}
\]
Maxwell’s Equations
From the Maxwell’s equations, the Fourier components of E and B satisfy
\begin{equation}
\vb{n} \times \vb{n} \times \vb{E} + \va{\va{K}} \cdot \vb{E} = 0.
\label{maxwell}
\end{equation}
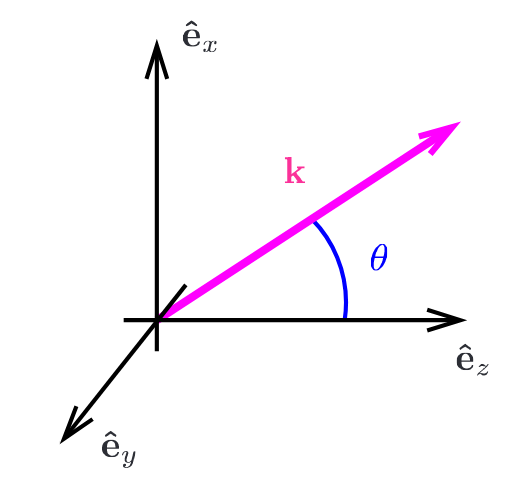
Assume that the propagation occurs only in (x,z) plane, i.e.
\begin{cases}
n_x = n \sin(\theta), \\
n_z = n \cos(\theta).
\end{cases}
Using the cold plasma dielectric tensor derived above, \eqref{maxwell} can be written in the form
\begin{equation}
\va{\va{M}}_{k,\omega} \cdot \mathbf{E} =
\begin{pmatrix}
S – n^2 \cos^2(\theta) & -iD & n^2 \cos(\theta) \sin(\theta) \\
iD & S – n^2 & 0 \\
n^2 \cos(\theta) \sin(\theta) & 0 & P – n^2 \sin^2(\theta)
\end{pmatrix}
\cdot
\begin{pmatrix}
E_x \\
E_y \\
E_z
\end{pmatrix}
= 0.
\end{equation}
The dispersion relation is therefore given by \(\abs{\va{\va{M}} }=0\), which can be recast in the form \[ An^4-Bn^2+C=0\] with
\begin{cases}
A = S \sin^2(\theta) + P \cos^2(\theta), \\
B = RL \sin^2(\theta) + PS(1 + \cos^2(\theta)), \\
C = PRL.
\end{cases}
In many cases, it is useful to write the dispersion relation as a quadratic in \(n_{\perp}^2\), considering \(n_{\parallel}^2\) is known:
\[A’ n_\perp^4 – B’ n_\perp^2 + C’ = 0\] with
\begin{cases}
A’ = S, \\
B’ = RL + PS – n_\parallel^2 (P + S), \\
C’ = P (n_\parallel^2 – R)(n_\parallel^2 – L).
\end{cases}
Lower Hybrid Wave: Arbitrary \(\theta\)
For the case with arbitrary \(\theta\), it would be significantly inconvenient to obtain an expression for the dispersion relation. However, if given \( \omega \approx\omega_{ci}\), approximation can be made to simplify the expressions.
Specifically, we have
\begin{align*}
A’ &= S, \\
B’ &\approx -\left(\frac{\omega_{pe}^2}{\omega^2}\right)(S – n_\parallel^2), \\
C’ &\approx -\left(\frac{\omega_{pe}^2}{\omega^2}\right)\left((S – n_\parallel^2)^2 – D^2\right)
\end{align*}
and thus the dispersion relation is obtained as
\begin{align*}
n_{\perp,F}^2 &= \frac{(n_{\parallel}^2 – R)(n_{\parallel}^2 – L)}{n_{\parallel}^2 – S}, \\
n_{\perp,S}^2 &= -\frac{P}{S}(n_{\parallel}^2 – S).
\end{align*}
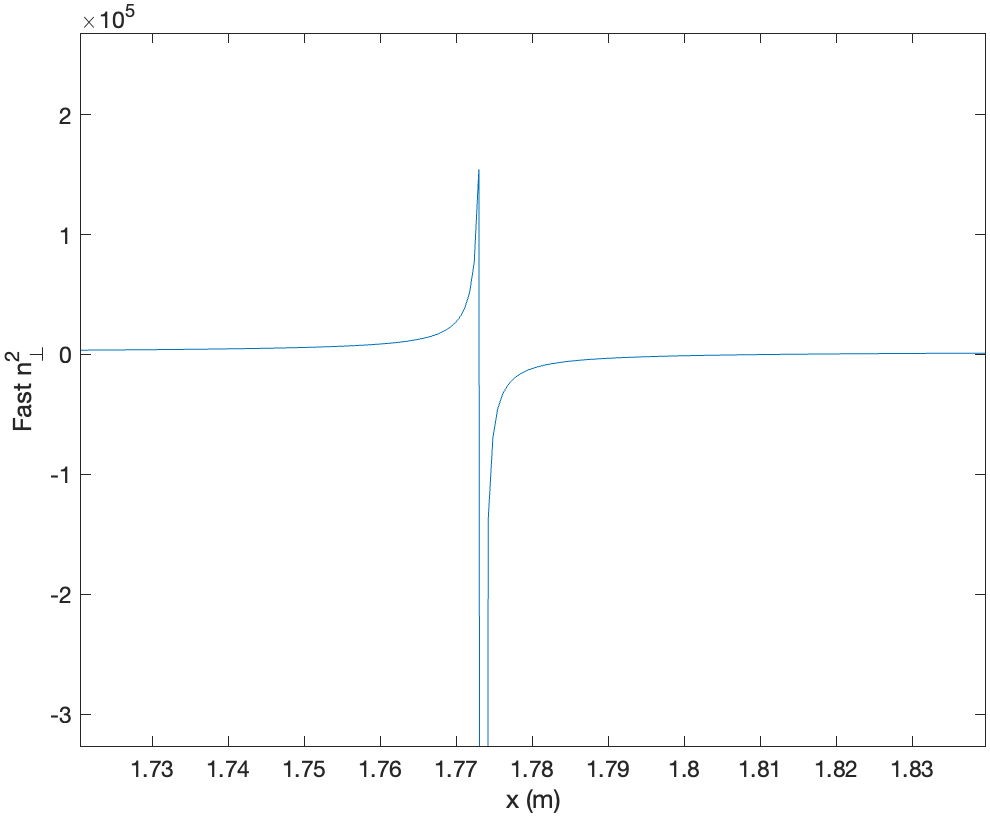
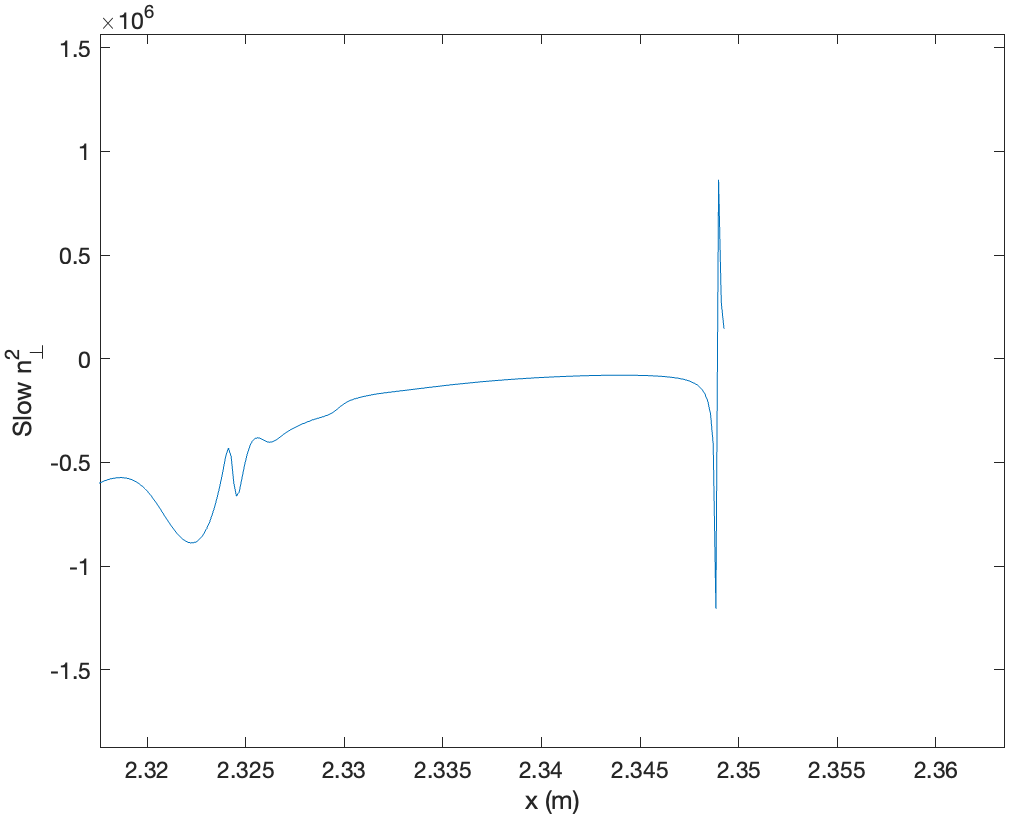
where S and F mean ‘slow’ and ‘fast’. Generally, \(n_S \gg n_F\), so their phase velocities (also frequency) satisfy F>S.
Due to the non-uniform B in Tokamaks, slow waves cannot propagate in the plasma (the cut-off is located around the plasma surface). A MATLAB code shows in the EAST tokamak, the fast wave resonates in the core area, whereas the slow wave resonates at the edge.